Loading [MathJax]/jax/output/HTML-CSS/jax.js

宇宙科学I (文科生)

太陽と地球

土井靖生

2019/10/4

今回のポイント

太陽は中心部の核融合により光っている
- 水素4つからヘリウム1つが合成
- 約100億年で中心部の水素を全てヘリウムに変換
  $\to$ 太陽の寿命は約100億年
太陽までの距離: 約1億5千万キロ=1天文単位(au)
太陽の表面温度: 約6000度
- 明るさはほぼ一定
- 可視光で一番明るく光る
- スペクトルの“吸収線”を調べると、ガスを構成する元素量が分かる
太陽表面の磁場による活動: 太陽フレア

太陽

太陽の諸定数

太陽の大きさ：直径約140万 km
- cf. 地球の直径: 4万km $/~\pi \simeq 12700$ km
- 地球の約110倍
太陽の重さ：約 $2 \times 10^{30}$ kg
- 地球の約33.3万倍
- 1 太陽質量 (Solar mass: $1~\mathrm{M}_{\odot}$ )
太陽までの距離：約1.5億km
- 1 天文単位 (Astronomical Unit: 1 au)
太陽の明るさ(光度)： $3.83 \times 10^{26}$ W
- 1 太陽光度 (Solar luminosity: $1~\mathrm{L}_{\odot}$ )

ひので最新観測画像より

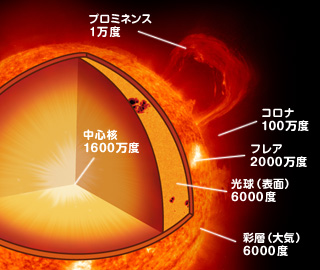
太陽の内部構造

水素7割、ヘリウム3割のガス球
エネルギー源は自己重力による高圧のため中心部で生じる核融合反応
- 毎秒 $3.7 \times 10^{38}$ 個の陽子(水素原子核)がヘリウム原子核に変換
- 合計質量は0.7%軽くなる
  $\to$ エネルギーに変換される
- $E = mc^2$
毎秒426万トンの質量が $3.8 \times 10^{26}$ Jのエネルギーに変換されている

©国立天文台/JAXA

太陽の寿命

寿命のうち約 9 割を主系列段階で過ごす。
主系列段階で全質量の 1割の水素を燃焼する。

上記より太陽の寿命の概算値を求めよ。

【情報】

太陽質量 $\mathrm{M}_{\odot} = 1.988 \times 10^{30}\ \mathrm{[kg]}$
太陽光度 $\mathrm{L}_{\odot} = 3.828 \times 10^{26}\ \mathrm{[J~s^{-1}]}$
光速 $\mathrm{c} = 2.998 \times 10^{8}\ \mathrm{[m~s^{-1}]}$
陽子質量 $m_p =1.673 \times 10^{-27}\ \mathrm{[kg]}$
ヘリウム原子核質量 $m_\alpha = 6.645 \times 10^{-27}\ \mathrm{[kg]}$

太陽までの距離の測り方

(天体の)距離の測り方

「ものさし」を当てる(直接測定)
“反射”を利用する
- 超音波、レーザー
三角測量

<span style='font-size:16px;position:relative;top:-60px'>星の距離の三角測量<br><span style='position:relative;top:-30px'>([Wikimedia commons](https://commons.wikimedia.org/wiki/File:Stellarparallax2.svg))</span></span>

星の距離の三角測量
(Wikimedia commons)

月のレーザー測距; 左：中国科学院ホームページより.
中：Apollo 11’s and 右：Apollo 15’s laser reflectors. [NASA]

ケプラーの法則
(Kepler’s laws)

ケプラーの惑星運動の法則
(Kepler’s laws of planetary motion)

ヨハネス・ケプラー（Johannes Kepler 1571–1630、ドイツの天文学者）
ティコ・ブラーエの観測記録から太陽に対する火星の運動を推定し、1619年に“ケプラーの法則”を発表 cf. コペルニクス「天体の回転について」(1543年)、ガリレオ裁判(1616年、1633年)

第1法則：楕円軌道の法則
第2法則：面積速度一定の法則
第3法則： $T^2 \propto r^3$
- 公転周期の2乗は軌道長半径の3乗に比例( $\propto$ は“比例”の記号)

Wikimedia commons

第3法則の導出

ニュートンはこの法則を参考に
万有引力の法則を導出(1686年)

遠心力 $f = \frac{mv^2}{r} \propto \frac{v^2}{r}$
引力 $f = G\frac{Mm}{r^2} \propto \frac{1}{r^2}$
周期 $T = \frac{2 \pi r}{v} \propto \frac{r}{v}$

遠心力=引力から $T^2 \propto r^3$ を得る

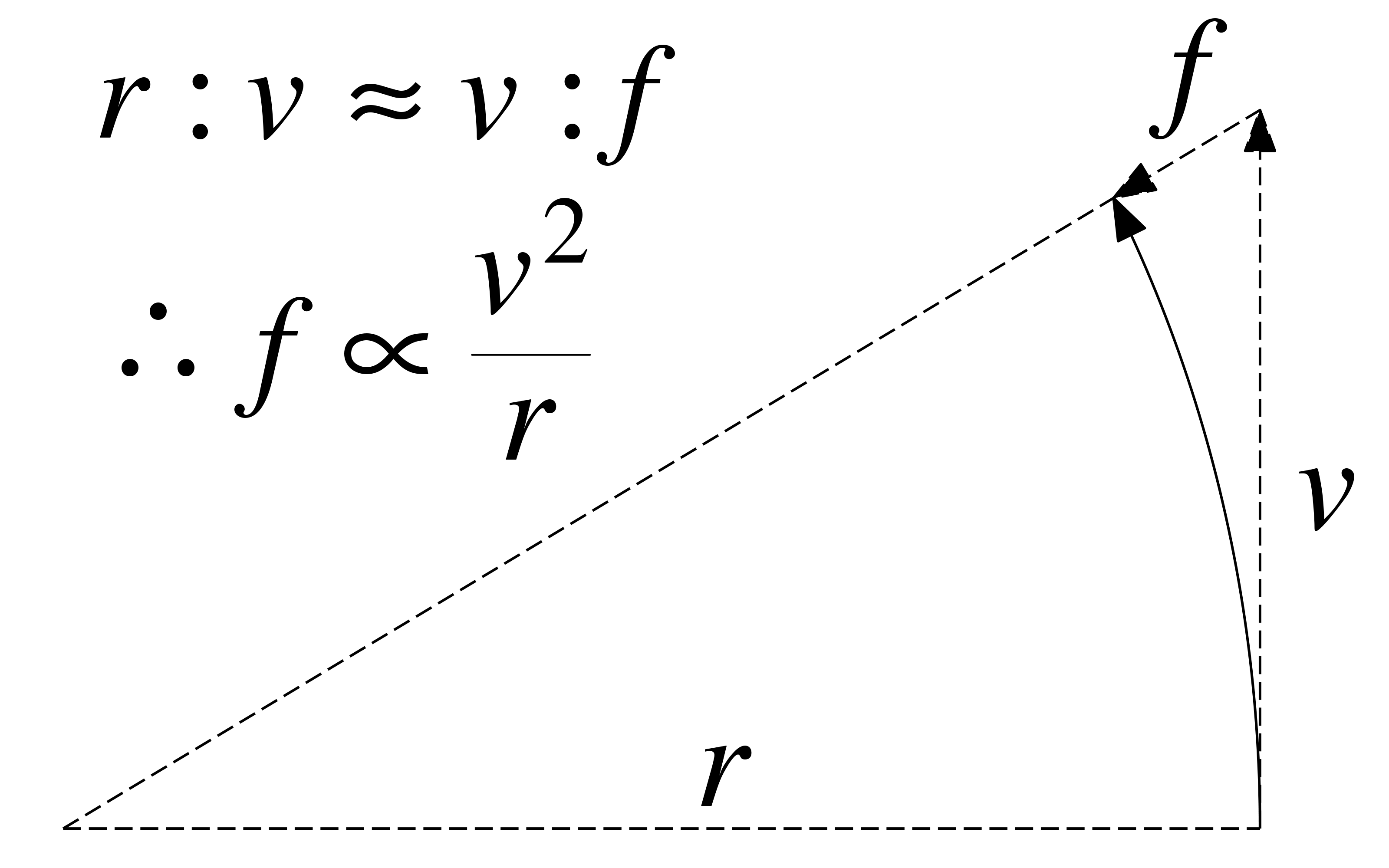
逆2乗則 (inverse square law)

力が逆2乗則に従う $\leftrightarrow$ 空間が3次元であることの証明

<span style="font-size:16px;position:relative;top:-60px">[Wikimedia commons](https://commons.wikimedia.org/wiki/File:Inverse_square_law.svg)</span>

Wikimedia commons

第3法則の応用

距離の測定

火星や金星の公転周期と地球の公転周期を比較
- $T^2 \propto r^3$ より“軌道半径の比”が求まる
レーザー測距により火星・金星までの距離を直接測定
地球の軌道半径 $=$ 太陽までの距離が求まる

質量の測定

軌道半径が分かれば、万有引力の法則から直接導ける

$1 \mathrm{M}_{\odot} = \frac{4 \pi ^2 \times \left( 1\mathrm{au} \right) ^3}{\mathrm{G} \times \left( 1\mathrm{yr} \right) ^2}$

【参考】質量の測定式の導出

$引力 = 遠心力より$

$\begin{align} f = G\frac{Mm \hspace{-0.7em} \backslash}{r^{2\hspace{-0.3em} \backslash}} &= \frac{m \hspace{-0.7em} \backslash ~ v^2}{r \hspace{-0.5em} \backslash}\\ \therefore M &= \frac{rv^{2}}{G}\\ \end{align}$

この式を $T=\frac{2 \pi r}{v}$ を用いて変形すると $M = \frac{4 \pi^2 r^3}{GT^2}$

但し万有引力定数 $G$ の値を精度良く知るのは難しい
(現在でもその精度は4桁程度)
天体の質量は通常「太陽質量の何倍か」と表現する

太陽スペクトル

赤外線の発見

ウィリアム・ハーシェル(William Herschel, 1738 - 1822)

ドイツ生まれ(後にイギリスに移住)音楽家/天文学者
天王星の発見(1781)、天の川銀河の構造の推測など
赤外線の発見(1800) “calorific light” $\to$ “infrared”

Science Museum, London / Science and Society Picture Library

Illustration by Vilmos Thernesz based on the original figure in Herschel, W., 1800: ”Experiments on the refrangibility of the invisible rays of the Sun” Phil. Trans. Roy. Soc. London 90, 284–292

Universal Histroy Archive/IPAC

太陽光のスペクトル

<span style="font-size:16px;position:relative;top:-50px">Image Credit: [Climate Science Investigations](http://www.ces.fau.edu/nasa/module-2/radiation-sun.php)</span>

Image Credit: Climate Science Investigations

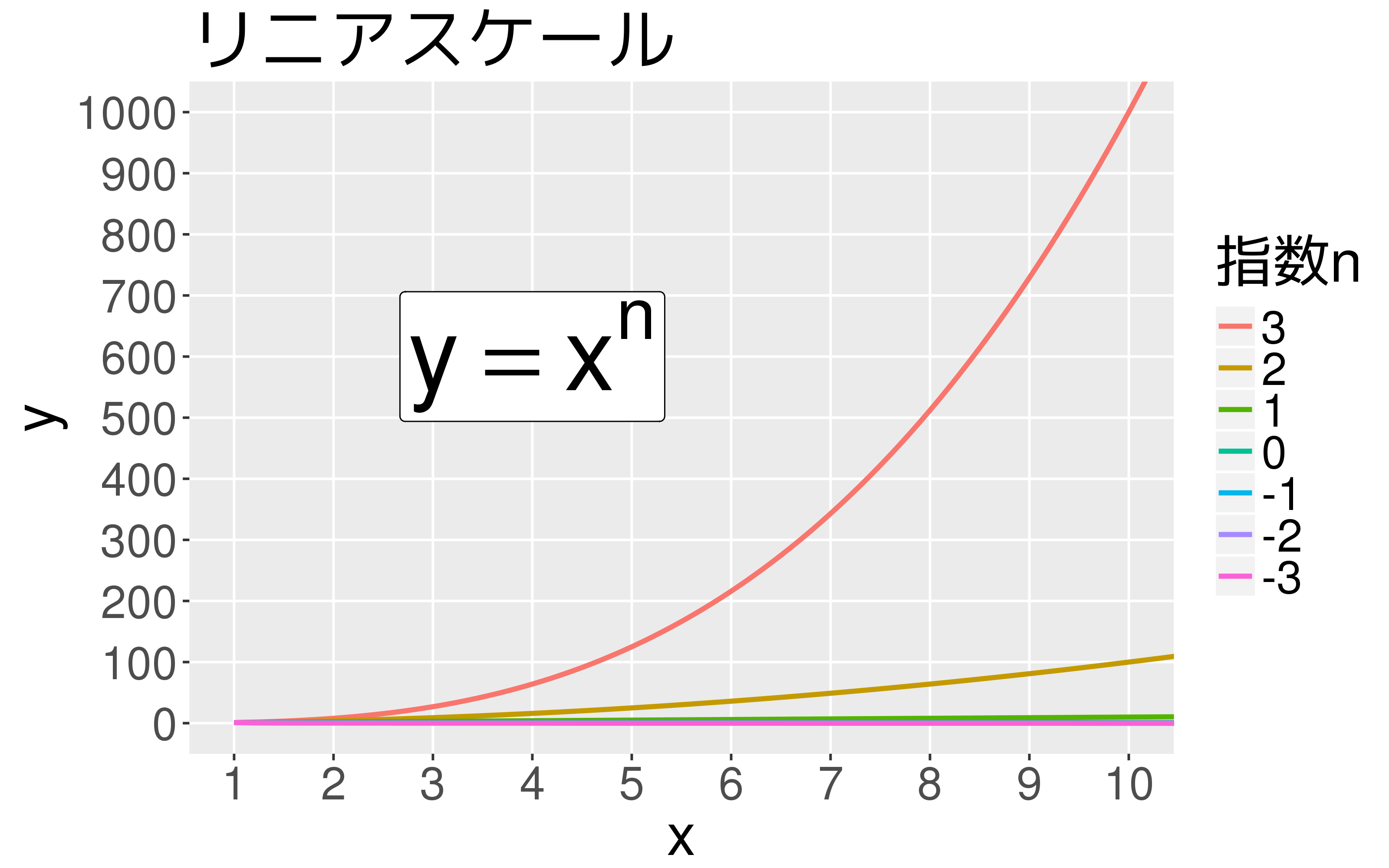
黒体輻射(温度によるスペクトルの違い)

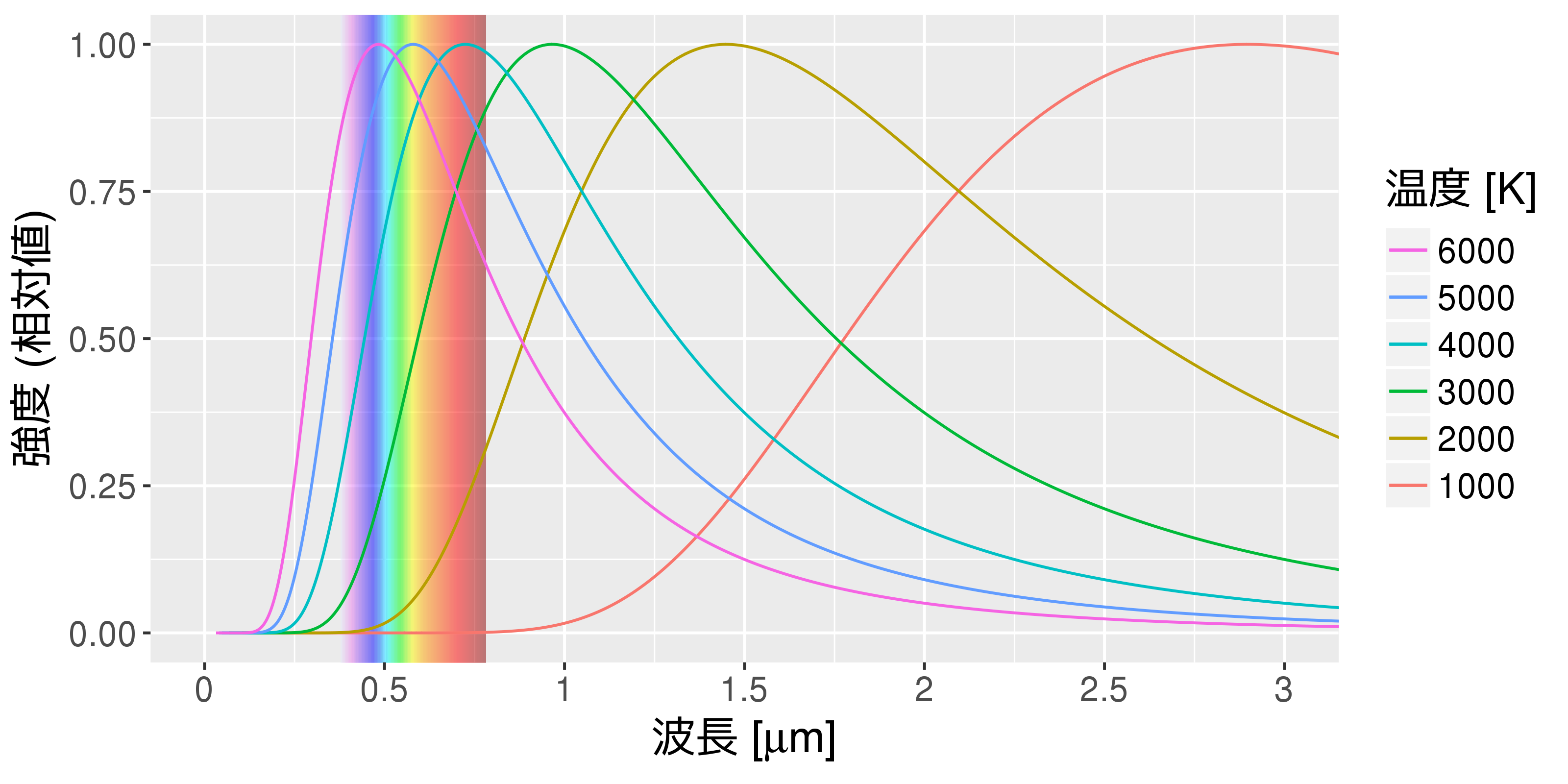
黒体輻射

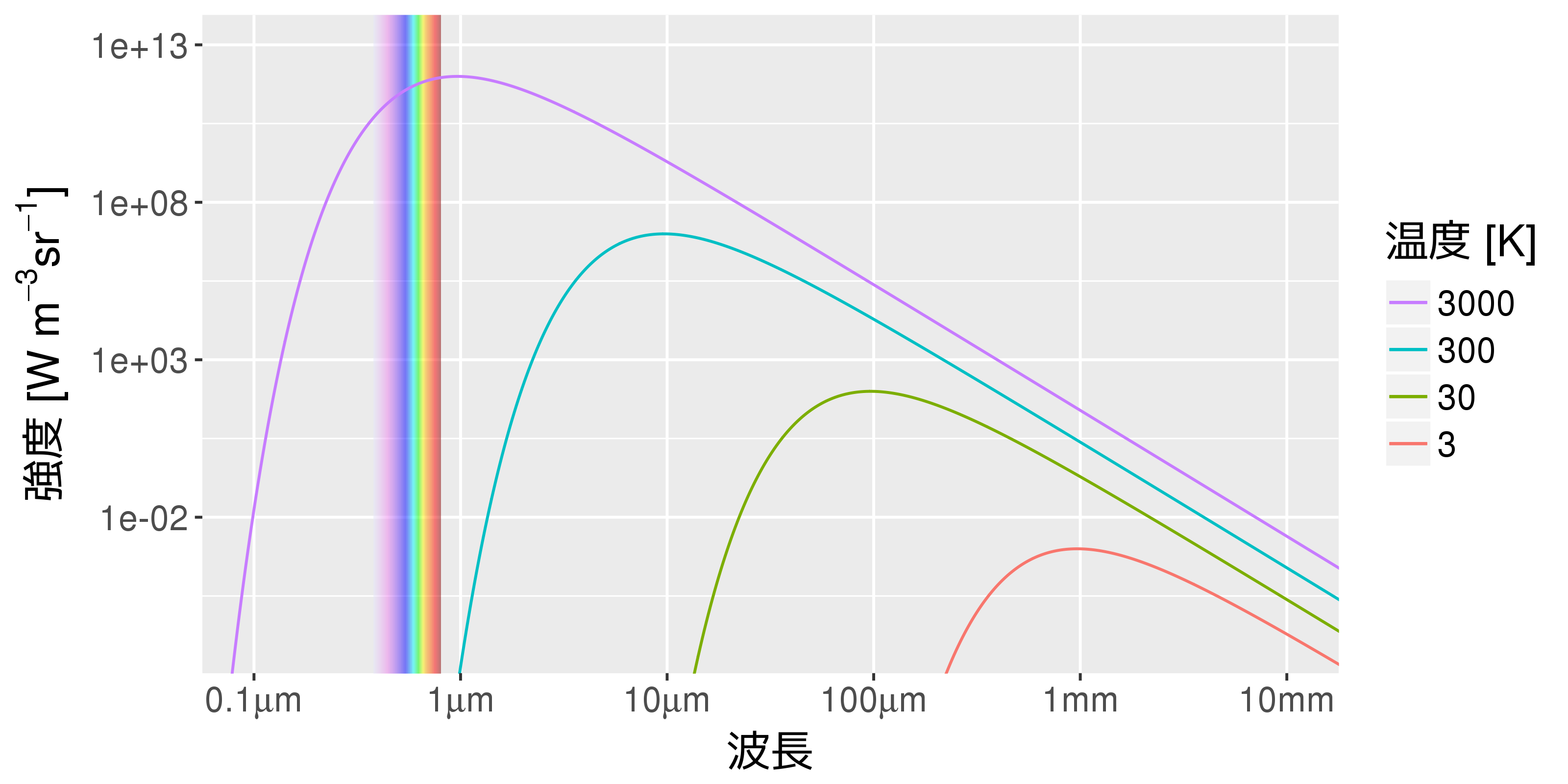
「リニアスケール」と「対数スケール」

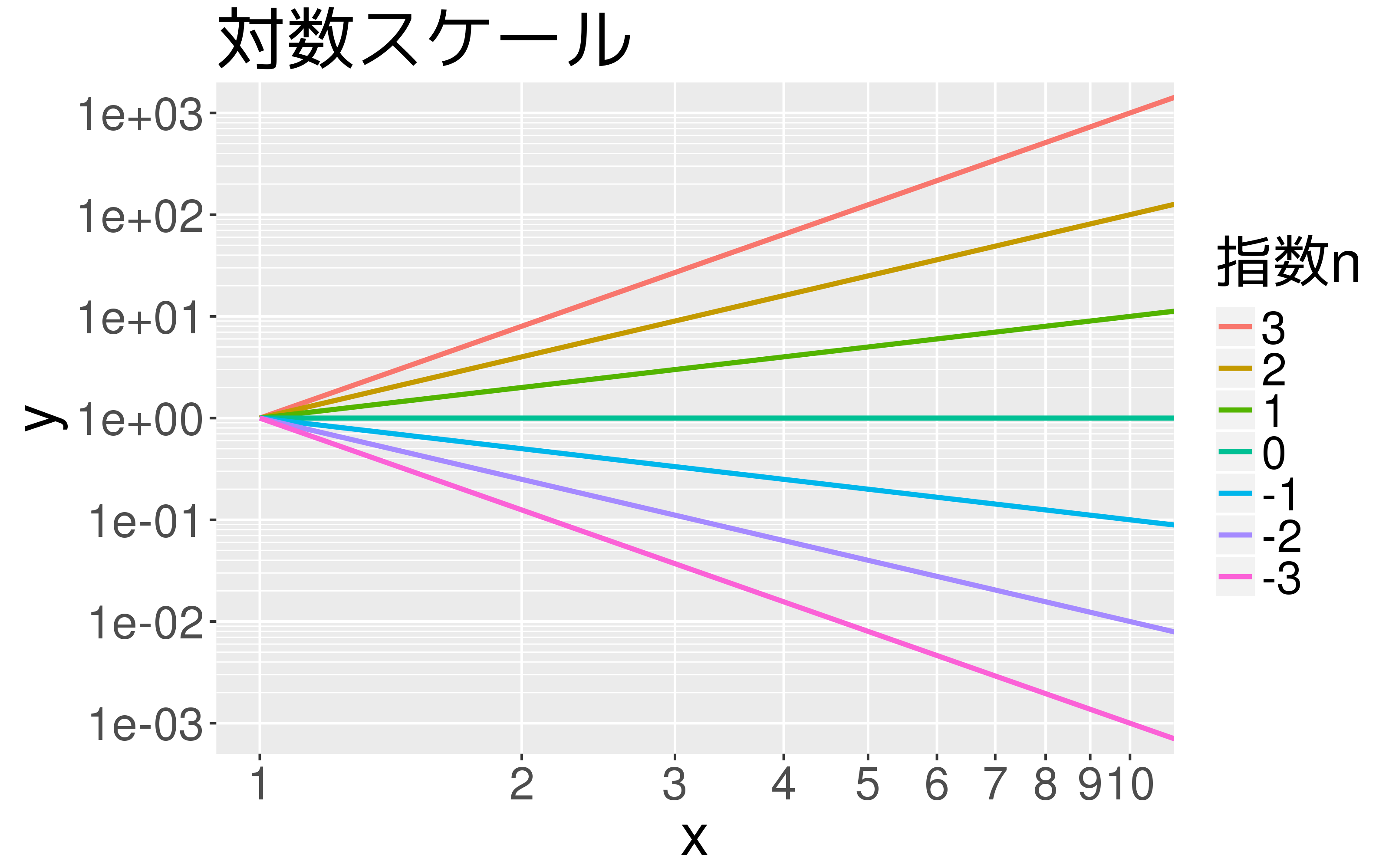
大気による吸収

<span style="font-size:16px;position:relative;top:-50px">Image Credit: [Wikipedia](https://en.wikipedia.org/wiki/Sunlight)</span>

Image Credit: Wikipedia

太陽の元素組成比

フラウンホーファー

太陽光スペクトルに暗線を観測(1814年, 発見は1802年イギリスのウォラストンが先)。彼の付けた記号と共に“フラウンホーファー線”と呼ばれる。

University of Oklahoma Libraries

By Deutsche Bundespost (scanned by NobbiP) [Public domain], via Wikimedia Commons

原子のエネルギー構造(水素原子の場合)

水素“原子模型”
(Bohr model)

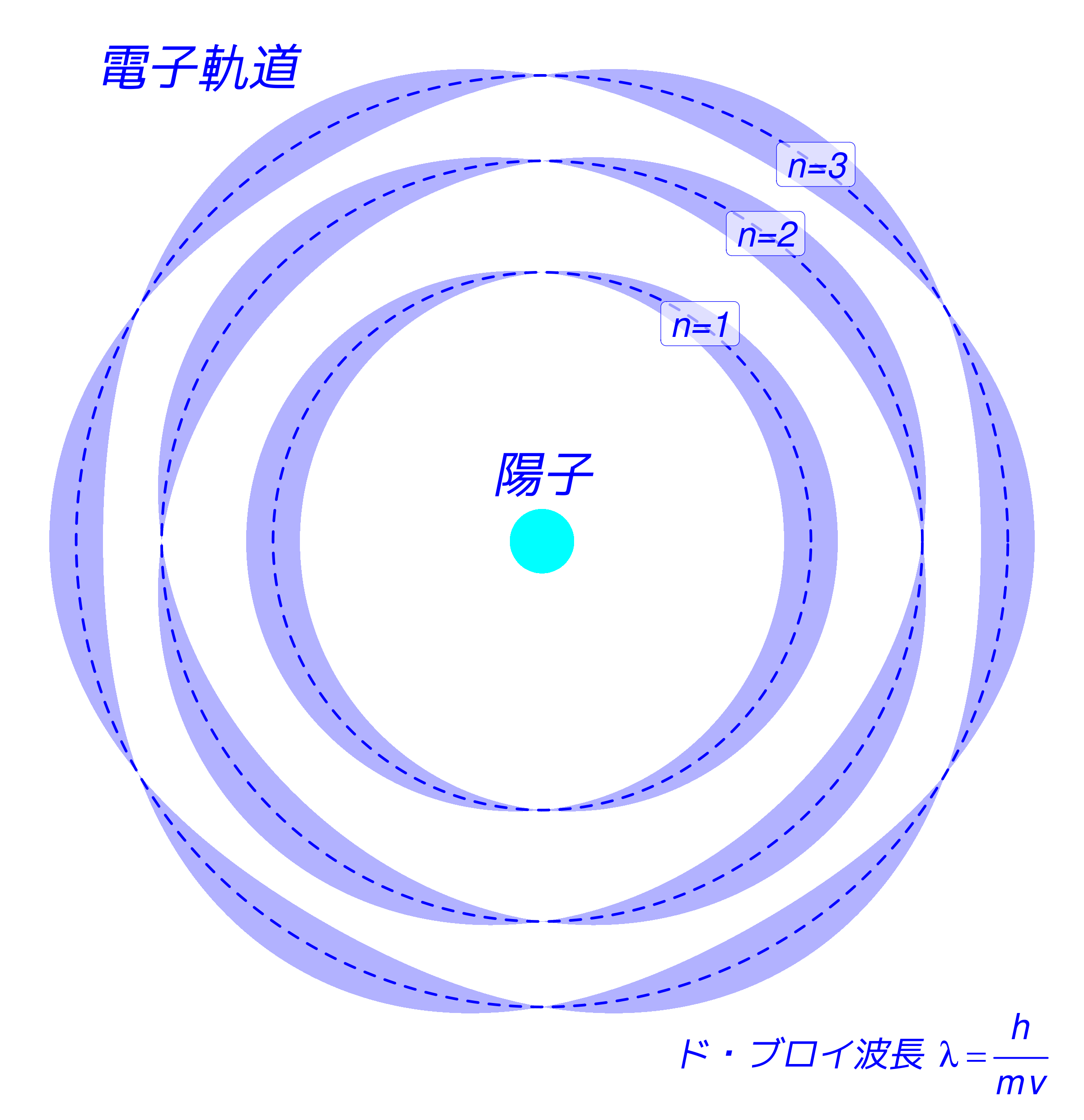
エネルギー準位と再結合線

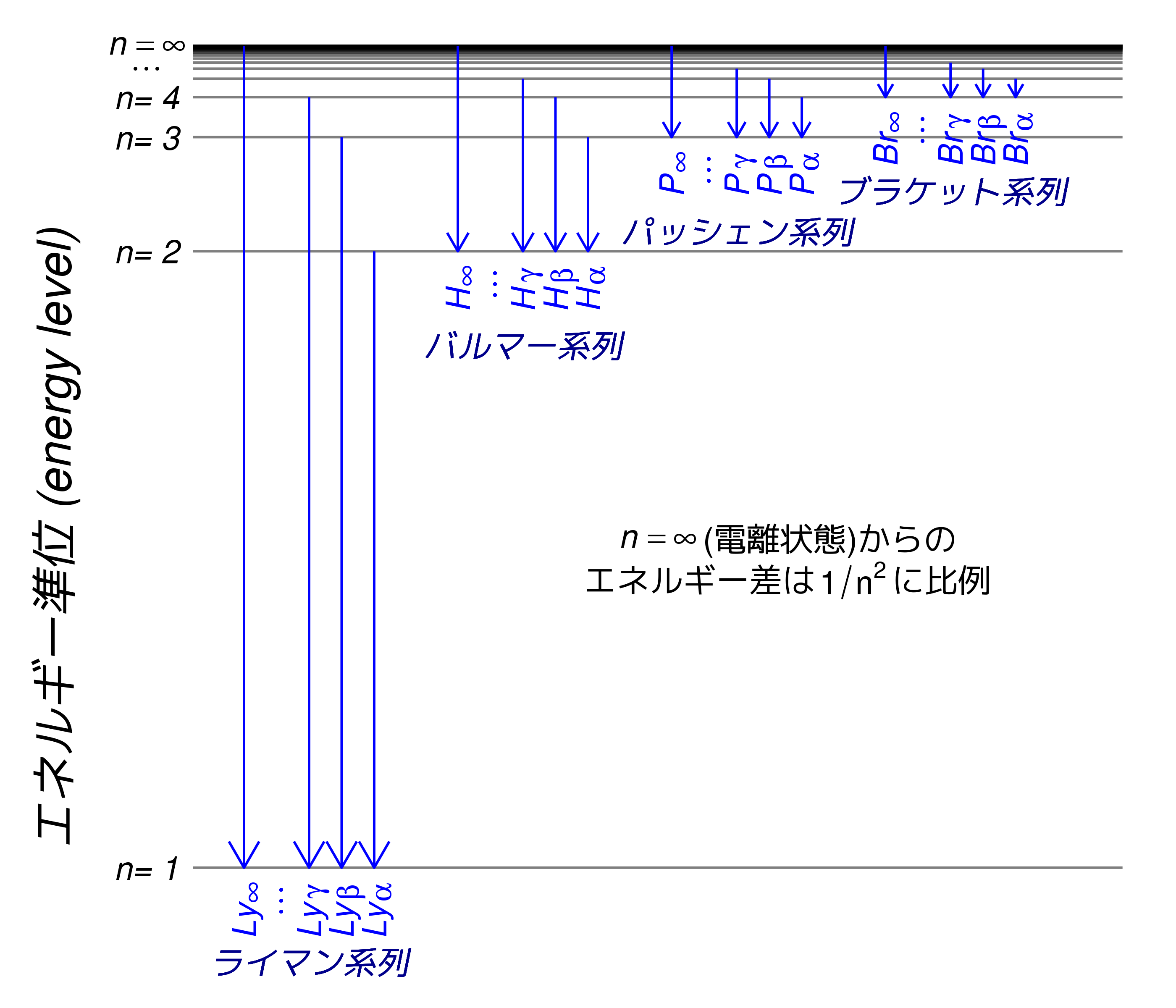
水素スペクトル線

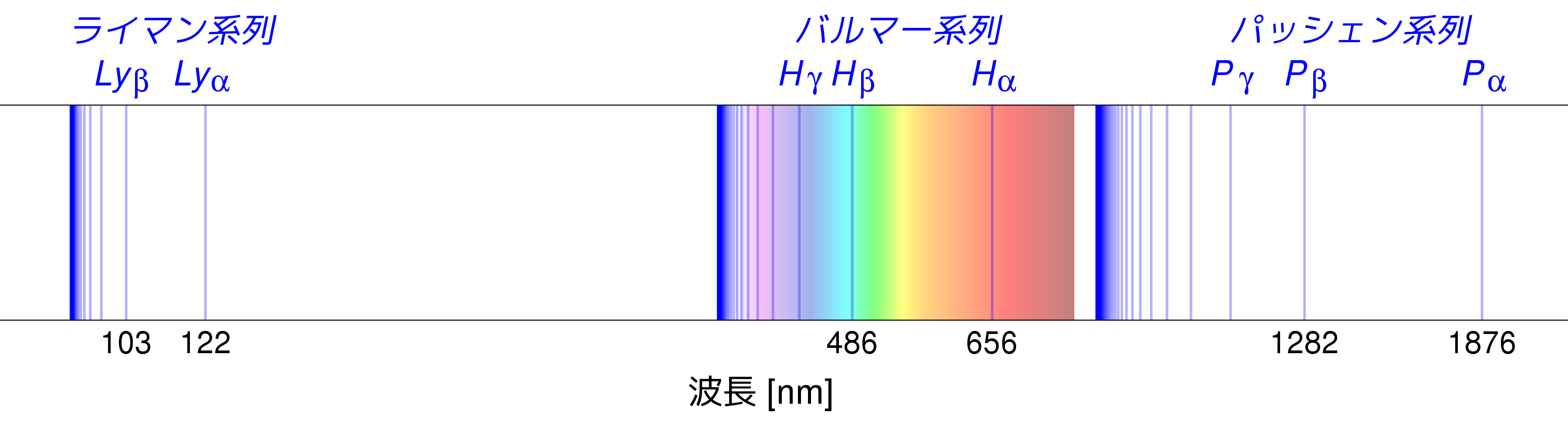
A low resolution spectrum of the star Vega showing prominently the Balmer lines of hydrogen.

(Martin, B./the King’s University College Astronomy Online)

フラウンホーファー線

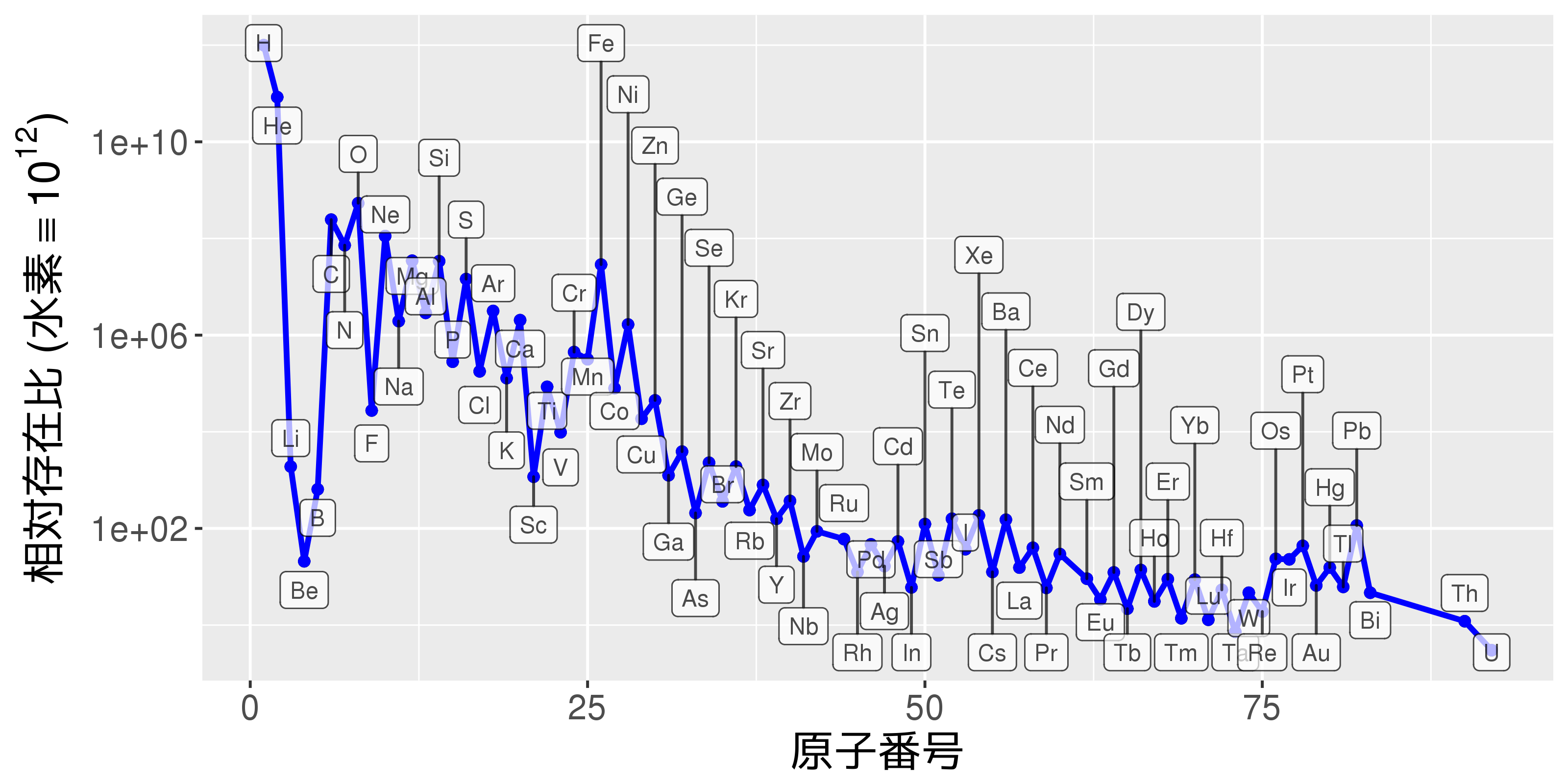
<span style="font-size:16px;position:relative;top:-60px">[Wikipedia](https://ja.wikipedia.org/wiki/%E3%83%95%E3%83%A9%E3%82%A6%E3%83%B3%E3%83%9B%E3%83%BC%E3%83%95%E3%82%A1%E3%83%BC%E7%B7%9A)</span>

元素の太陽存在比 (solar abundance)

太陽の分光観測や太陽風の直接観測などから推定
宇宙の元素存在比を考える上で基本となる量

data from Lodders (2010)

太陽の内部構造

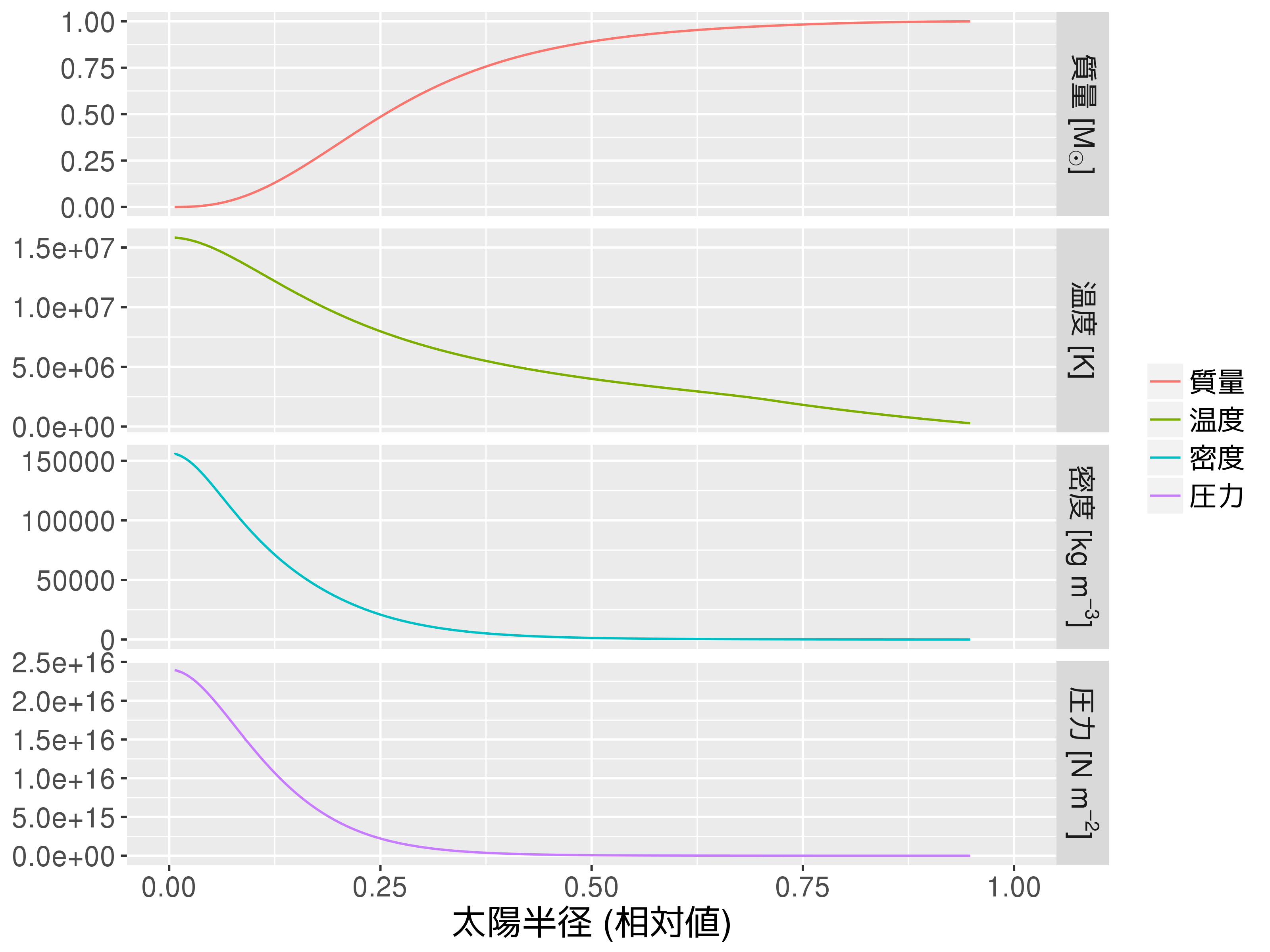
標準太陽モデル

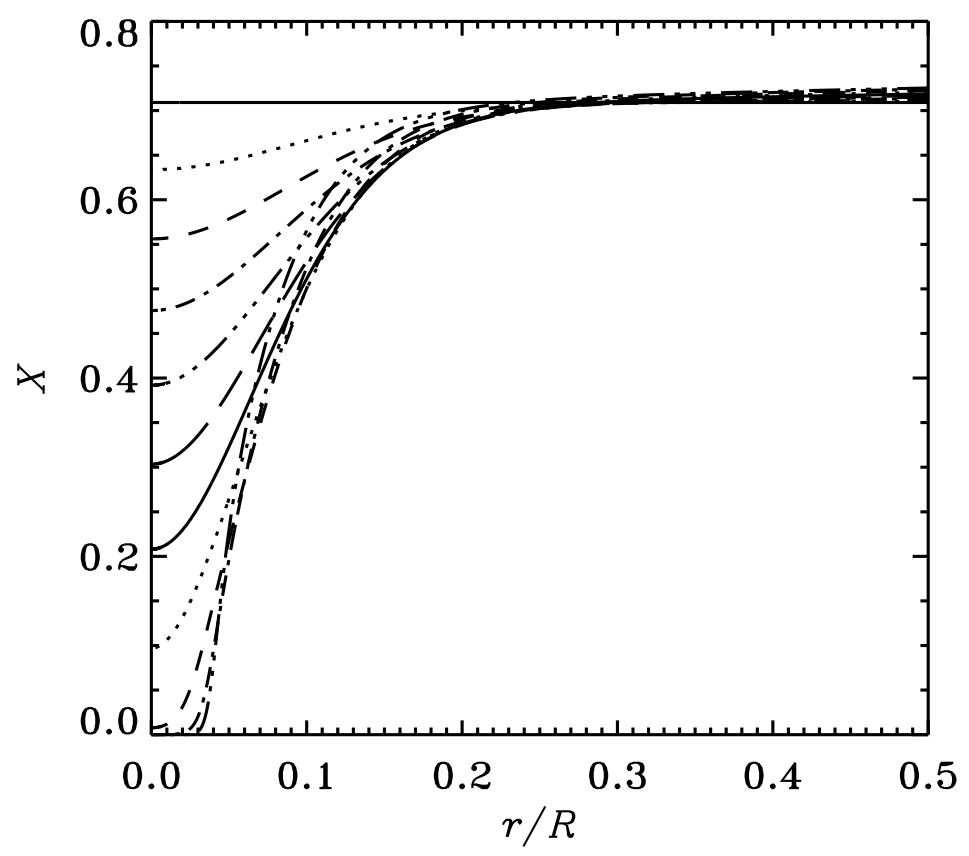
Bahcall and Pinsonneault: Rev. Mod. Phys., 67, 781, 1995

標準太陽モデル(元素組成比)

Bahcall and Pinsonneault: Rev. Mod. Phys., 67, 781, 1995

太陽の年齢と寿命

Christensen-Dalsgaard (2009)

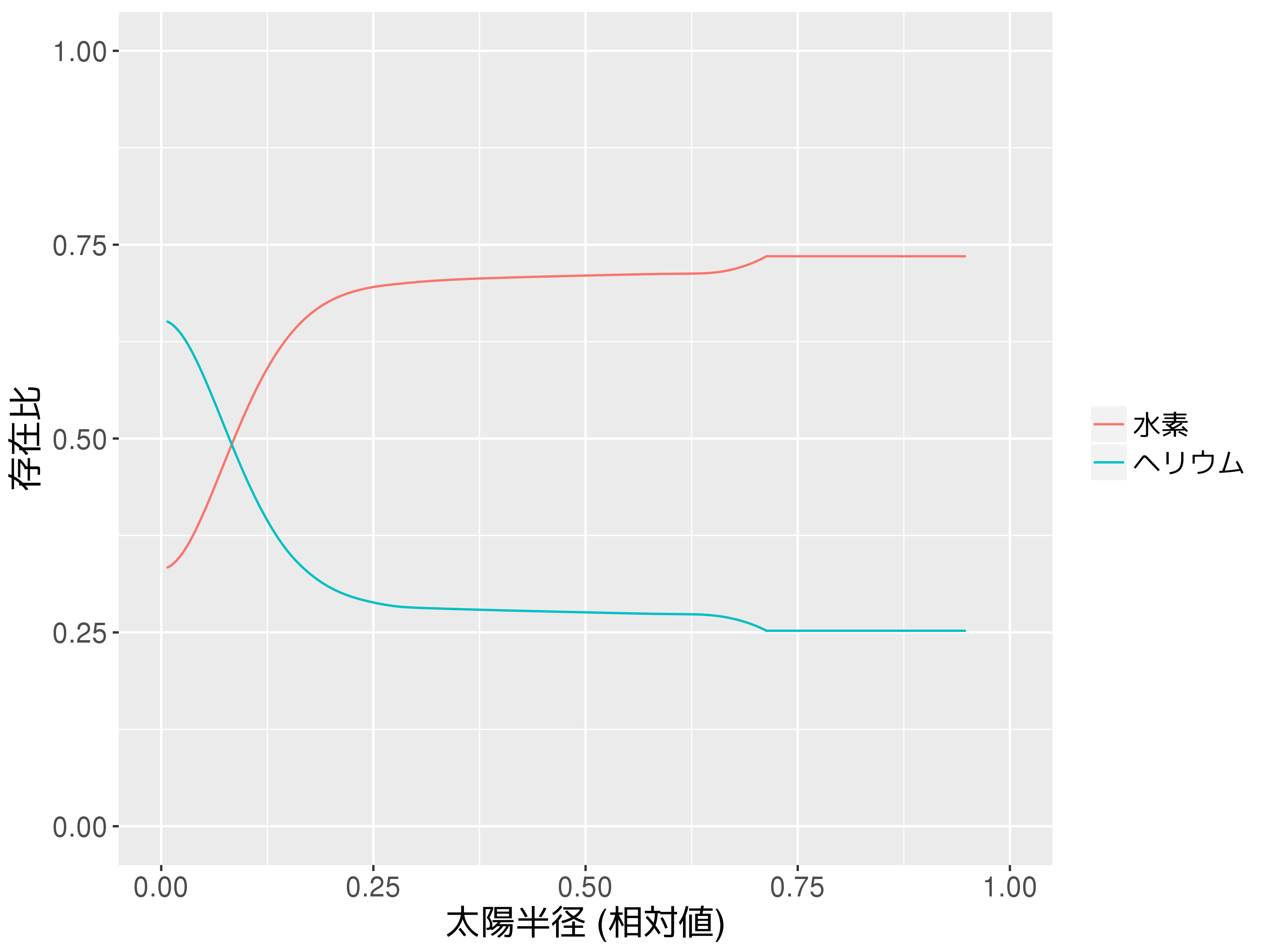
横軸: 半径(太陽半径で規格化)
縦軸: 水素の重量比
各線は 10 億年毎 (0-100 億年)

現在の太陽中心部のH存在比は $0.33$ と推測される。 $\to$ 現在の太陽年齢は約46億年

cf. 最も始原的な隕石の年齢は $45.672\pm0.005億年$

太陽の寿命は約100億年

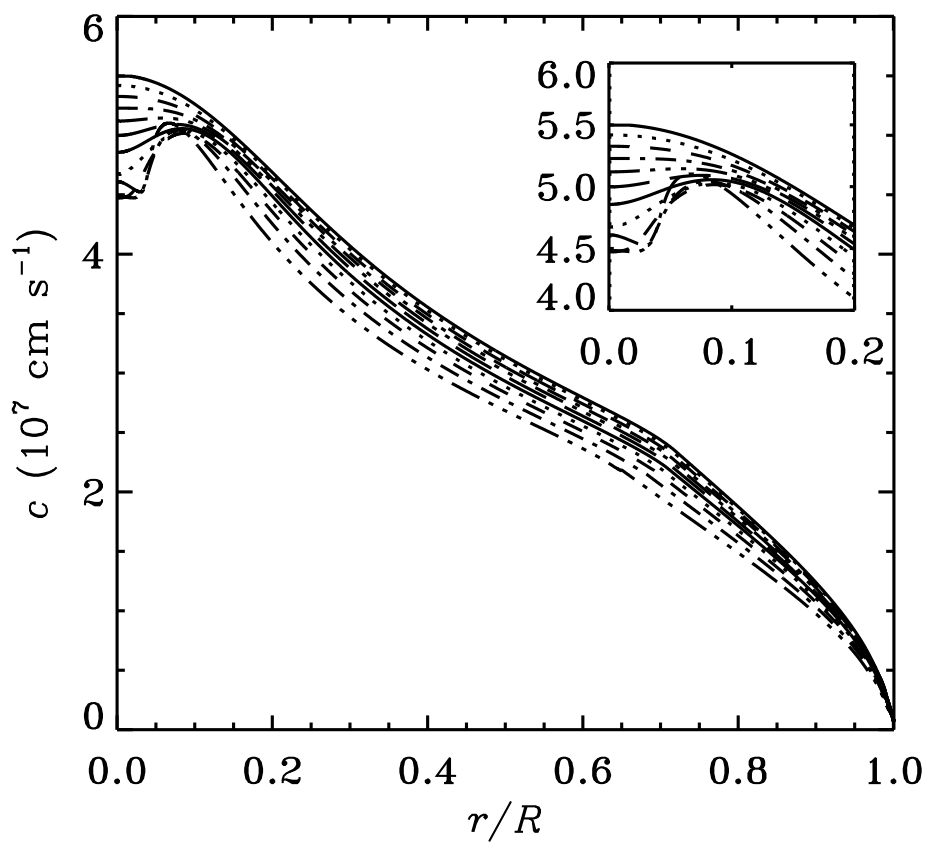
日震学(helioseismology)による年齢決定

太陽表面は約5分周期で振動している
中心部の組成変化により圧力分布が変わる
振動周期を分析し、内部の圧力分布を知る $\to$ 日震学

Christensen-Dalsgaard (2009)

人工衛星による太陽観測

太陽観測衛星

<span style="font-size:16px;position:relative;top:-50px">[Scholarpedia](http://www.scholarpedia.org/article/Solar_Satellites)</span>

日本の太陽観測衛星

ひのとり(ASTRO-A)
- 1981年 – 1991年
- M-3Sロケット2号機
- 質量: 188kg
ようこう(SOLAR-A)
- 1991年 – 2001年(2004年)
- M-3SIIロケット6号機
- 質量: 約390kg
ひので(SOLAR-B)
- 2006年 –
- M-Vロケット7号機
- 質量: 900kg

<span style="font-size:16px;position:relative;top:-50px">[ISAS/JAXA](http://www.isas.jaxa.jp/ISASnews/No.262/hajime.html)</span>

望遠鏡サイズと分解能

$\theta \simeq \frac{\lambda}{D}$ が最小分解能
- $\theta$ : 最小分解能
- $D$ : 望遠鏡の口径(直径)
- $\lambda$ : 観測する光の波長
$D$ が大きい方が分解能良い
$\lambda$ が小さい方が分解能が良い

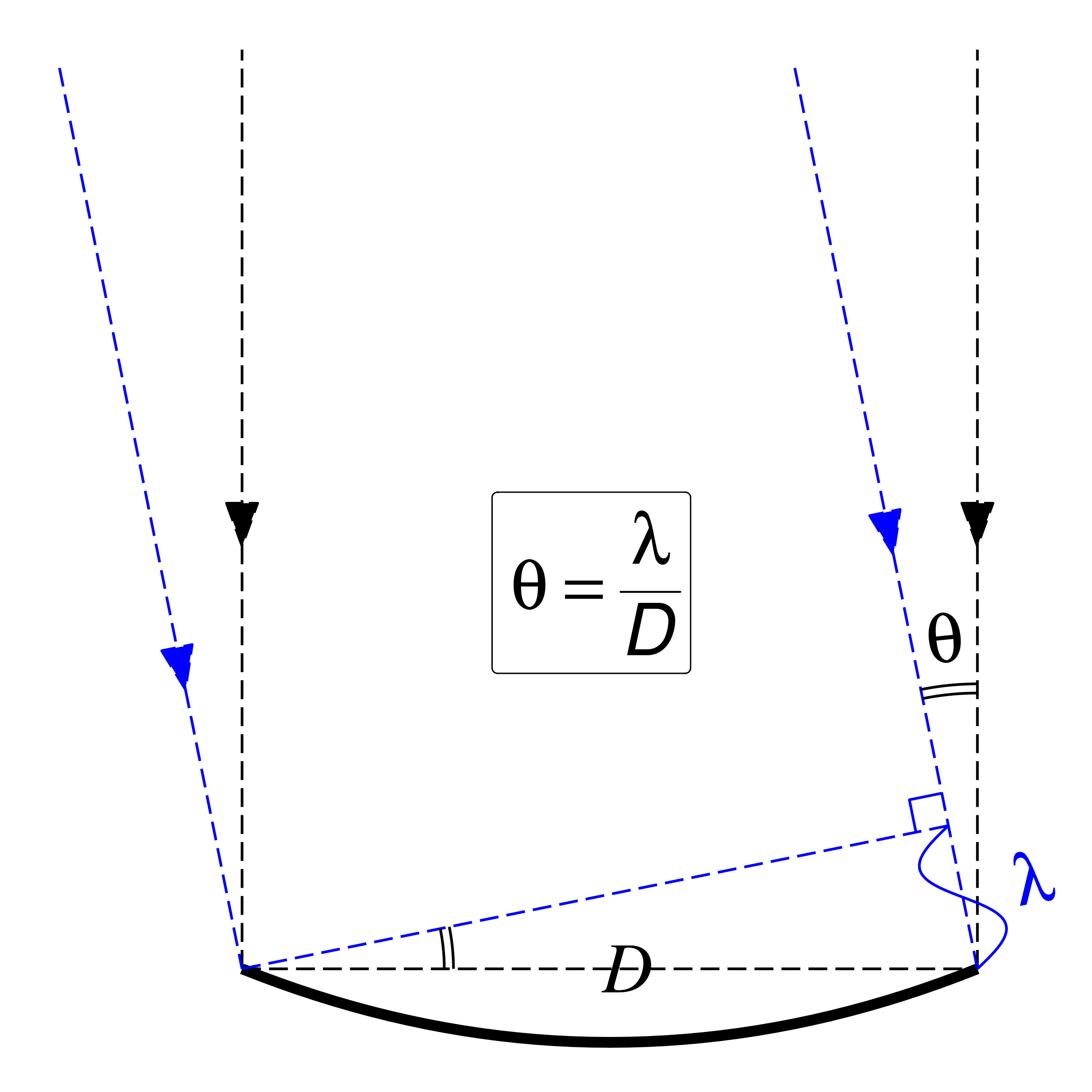
このことだけを考えると、人工衛星を飛ばすよりも地上に大きな望遠鏡を置いた方が都合が良い。

人工衛星で観測する理由1

大気揺らぎの影響を避ける
- ex. ハッブル宇宙望遠鏡

左図: レアンドロ・エルリッヒ『スイミング・プール』2004年　金沢21世紀美術館　(c) Leandro ERLICH　撮影：渡邉修

右図: Image credit: NASA

地上 vs. 宇宙

<span style="font-size:16px;position:relative;top:-50px">[Credit: NASA, Mauro Giavalisco, Lexi Moustakas, Peter Capak, Len Cowie and the GOODS Team.](http://hubblesite.org/image/1461/news/56-hubble-telescope)</span>

Credit: NASA, Mauro Giavalisco, Lexi Moustakas, Peter Capak, Len Cowie and the GOODS Team.

補償光学 (adaptive optics)

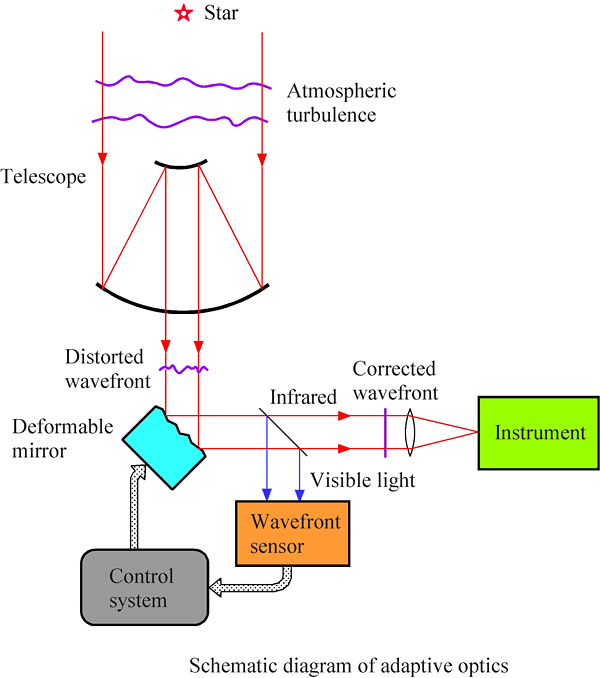
補償光学 (adaptive optics)

UCLA Galactic Center Group / W. M. Keck Observatory Laser Team

人工衛星で観測する理由2

地上から観測の不可能な波長を見る

<span style="font-size:16px;position:relative;top:-50px">[Salvetti, D. 2016, arXiv:1603.00231](https://arxiv.org/abs/1603.00231)</span>

Salvetti, D. 2016, arXiv:1603.00231

太陽活動と磁場

ひのでによる太陽の観測

JAXA, NAOJ ISAS/JAXA

荷電粒子の磁力線への巻きつき

Il campo magnetico della Terra

立花隆ゼミホームページより

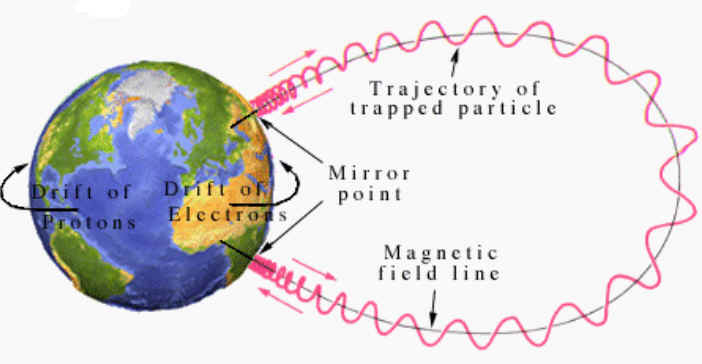
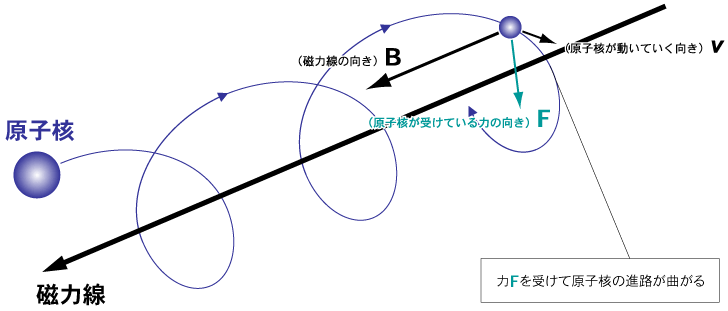
プラズマ(荷電粒子)は磁力線に沿ってしか動けない

$\to$ プラズマの磁力線への“凍結”

コロナ加熱問題

太陽の表面温度(光球温度)：6000[K]
コロナの温度：100万[K]

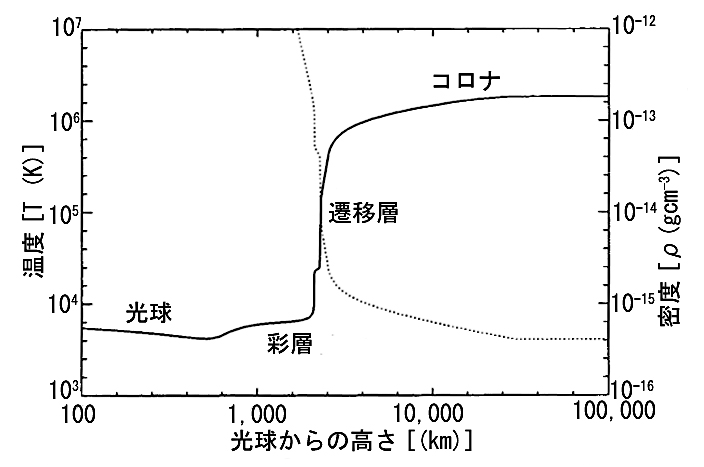
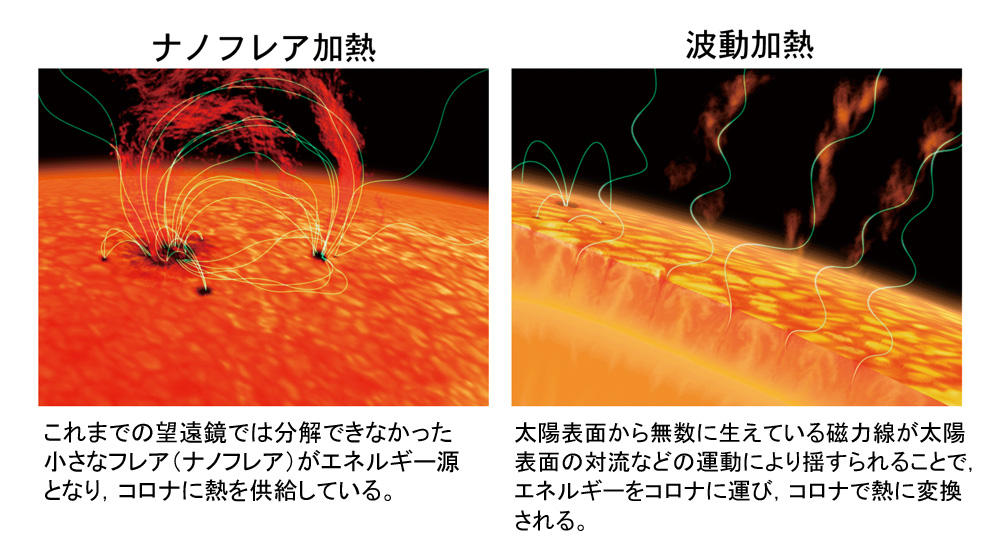
ひのでによる彩層の観測

<span style="font-size:16px;position:relative;top:-60px">[HINODE/CLASP](http://hinode.nao.ac.jp/KakenS/study-CLASP-2.shtml)</span>

磁気波動による加熱

HINODE観測画像(グラニュールとスピキュール)

Matsumoto & Suzuki 2014, MNRAS, 440(2), 971–986

太陽フレア

黒点と磁場

<span style="font-size:16px;position:relative;top:-60px">[Min S. Yun 氏ホームページより](http://www.astro.umass.edu/~myun/teaching/a100_old/longlecture11.html)</span>

Min S. Yun 氏ホームページより

太陽フレアの成因

黒点付近のねじれた磁場のリコネクションとする説が有力

「ようこう」によるカスプ構造の発見

「ようこう」最大の成果のひとつ : フレアのエネルギー解放過程が磁気リコネクションであることをほぼ決定づけた (ISASニュース2003年1月号『特集：「ようこう」の10年』)

<span style="font-size:16px;position:relative;top:-40px">[ISAS/JAXA](http://www.isas.jaxa.jp/ISASnews/No.262/chap4-03.html)</span>

CME

地球への影響

<span style="font-size:16px;position:relative;top:-40px">[NICT](https://academist-cf.com/journal/?p=4717)</span>

Aurora

地球への影響の例

1989年3月13日の磁気嵐

3日前のX15クラスのフレアにより発生
カナダで変電所の変圧器を破壊、9時間に亘る大停電を引き起こしたとされる

GOES-7 monitors the space weather conditions during the Great Geomagnetic storm of March 1989

観測史上最大のフレア

記録上最大の磁気嵐

1859年9月1日にキャリントン(イギリスの天文学者)により観測される(キャリントン・フレア)
9月1日から2日にかけて記録上最大の磁気嵐が発生
ハワイやカリブ海沿岸等の低緯度地域を含む世界中で強いオーロラが観測される
ヨーロッパおよび北アメリカ全土の電報システムが停止するなどの影響
磁気嵐の強度“disturbance storm time”
Dst = -800 nT – -1750 nT と推定される

Carrington-Class Solar Storm

宇宙天気予報

Academist Journal

宇宙環境計測情報システム

宇宙天気情報センター

スーパーフレア

過去最大のフレアの更に100倍 $\sim$ 1000倍のフレアが観測される
発生頻度は $800 \sim 5000$ 年に一度

マイナビニュース

Solar Dynamics Observatory

NASA’s Goddard Space Flight Center

太陽の活動サイクル

11年周期

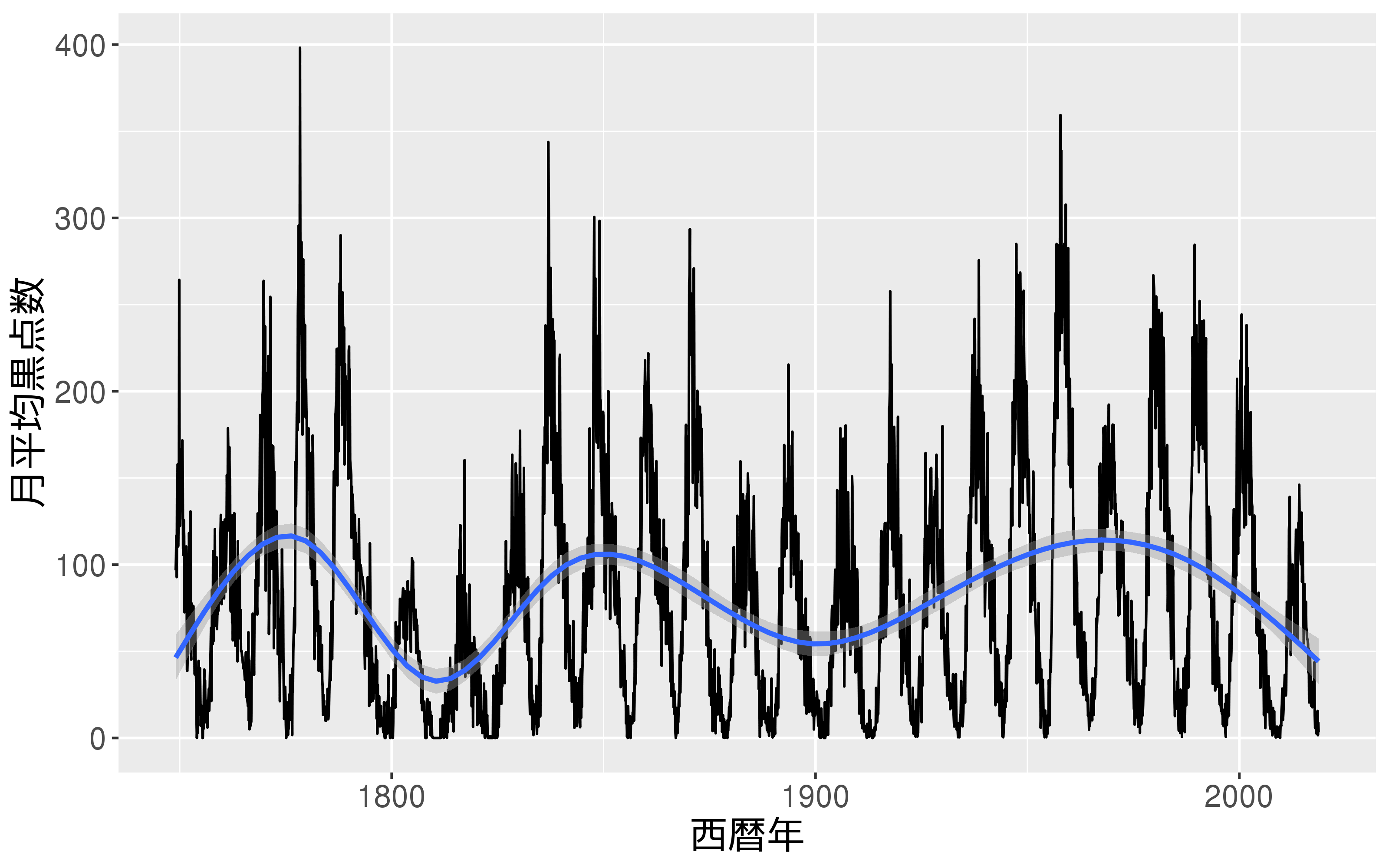
太陽定数の変化

<span style='font-size:16px;position:relative;top:-40px'>[NASA](https://science.nasa.gov/science-news/science-at-nasa/2009/01apr_deepsolarminimum)

太陽定数と気候変動との関わり

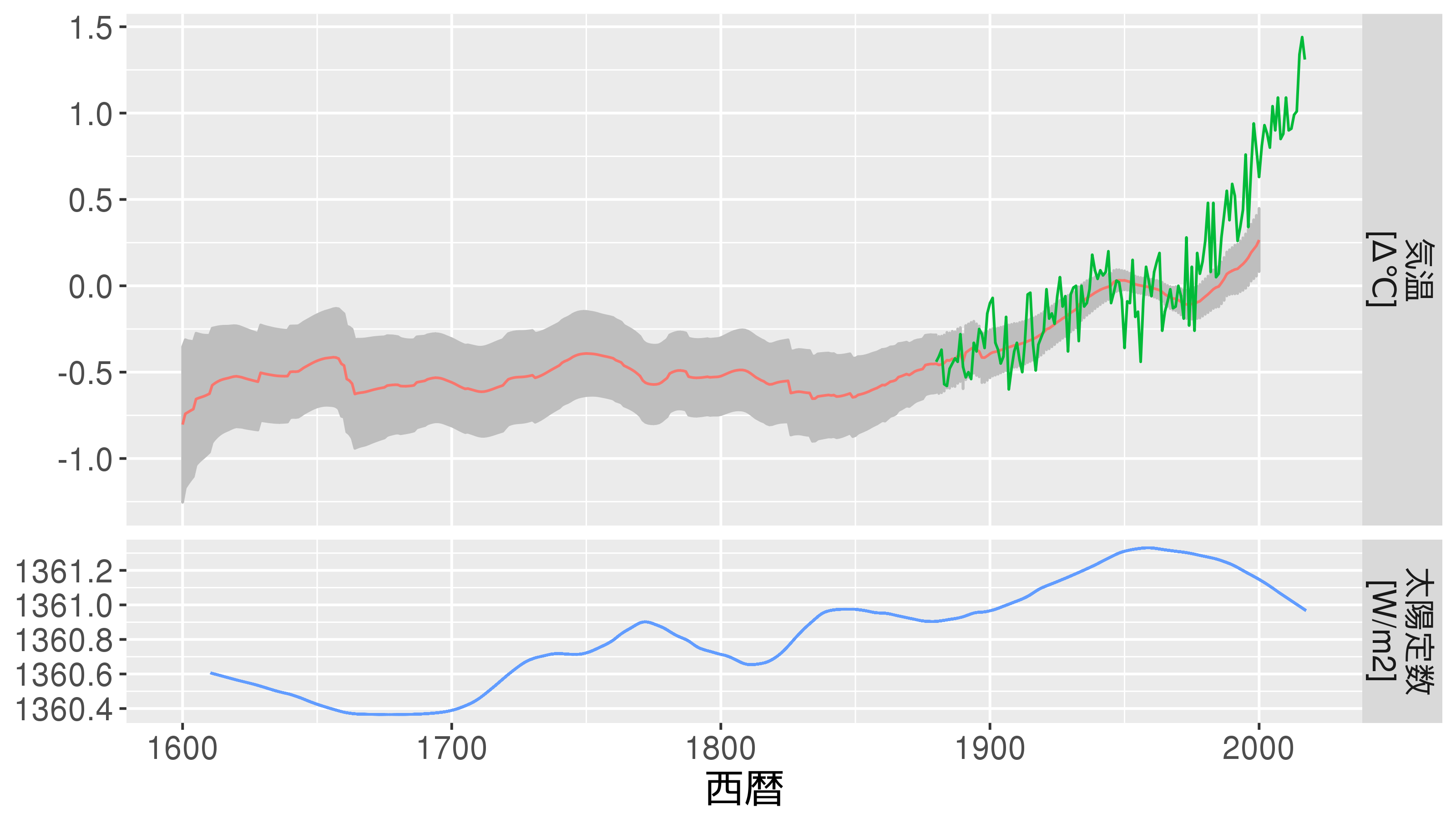
TSI data from THE SUN AND THE EARTH’S CLIMATE, and temperature data from Leclercq and Oerlemans 2012 & NOAA National Centers for Environmental information

Winter in Europe “the Little Ice Age”

Avercamp, ca.1608

Avercamp, ca.1620

太陽定数と地球のエネルギー収支

天頂にある太陽から受け取るエネルギー(太陽定数)：
約 $1366\ [\mathrm{W/m}^2]$ (0.1%程度の変動あり)
太陽から受け取るエネルギー総量： $1.75\times 10^{17} \mathrm{[W]} = 175 \mathrm{[PW]}$
地熱エネルギー：
約 $44 \mathrm{[TW]}$ = 太陽エネルギーの約0.025%
潮汐によるエネルギー：
約 $3 \mathrm{[TW]}$ = 太陽エネルギーの約0.002%
人類によるエネルギー消費(2017年)：
$17.926 \mathrm{[TW]}$ = 太陽エネルギーの約0.01%
[参考]マグニチュード9.0の地震エネルギー： $E = 10^{4.8 + 1.5 \times M} = 2\times 10^{18} \mathrm{[J]}$
(人類のエネルギー消費1.3日分)

1

宇宙科学I (文科生) 太陽と地球土井靖生 2019/10/4