宇宙科学I (文科生)
星の進化と終末
土井靖生
2019/10/25,11/1
今回のポイント1/4
- 星の一生、特にその晩年の様子を述べます
- 星の死に方は星の重さで決まる
- 軽い星から順に「惑星状星雲+白色矮星」「超新星爆発+中性子星」「超新星爆発+ブラックホール」
- 「主系列星」: 中心部で水素の核融合を起こしている星
- 星は一生の大半を「主系列星」として過ごす
- 「赤色巨星」: 中心部の水素が全てヘリウムに変換
- 中心部の周り(より外側)で水素核融合
- この時星の表面から全体の2割以上のガスが流れ出す
\(\to\)「惑星状星雲」となる - 軽い星はここで一生を終える
今回のポイント2/4
- 「赤色超巨星」: ヘリウムの核融合
- 太陽程度\(\sim\)太陽の8倍程度の重さの星は中心部でヘリウムの核融合が起こる
- ヘリウムから炭素や酸素が合成される
- 水素核融合時と同様の現象が進む
- ただしヘリウムは水素に比べて\(1/10 \sim 1/100\)の時間で燃え尽きる
- 「赤色超巨星」となり、表面から激しくガスが流出
\(\to\)熱い中心核がむき出しとなる:「白色矮星」 - 「白色矮星」内部では核融合は終了。徐々に冷却して星の一生を終える。
今回のポイント3/4
- 「超新星爆発」: 太陽の8倍よりも重たい星の最期
- 炭素核融合により、より重たい元素合成が起こる
- 鉄が出来たところで核融合がストップ・「超新星爆発」が起こる
- 中心核は「中性子星」として残る
- 距離指標としての巨星・超巨星
- 特注的な周期で明るさが変化: 「変光星」
- 星の明るさと変光周期を測ると、星までの距離を知ることが出来る
- 「年周視差」は我々の銀河系内部の距離が測れる
- 「変光星」は近くの銀河までの距離が測れる
今回のポイント4/4
- 距離指標としての超新星爆発
- 「白色矮星」に隣の星からガスが限界を超えて降り積もると、潰れて「中性子星」となる
- この時起こる超新星爆発は一定の明るさ\(\to\)我々から見た明るさと比較することで距離を知ることが出来る
- かなり遠方の銀河までの距離を測れる
- 水素・ヘリウム以外の(ほとんどの)元素は星で作られる
- 核融合で出来た“重元素”が巨星・超巨星からの“質量放出”により宇宙空間に撒かれる
- 超新星爆発時に“重元素”が放出される
- 中性子星と中性子星が合体した時にも多くの元素が合成される
主系列星
(main sequence stars)
主系列星
- 中心部で水素の核融合が進行
- ppチェインとCNOサイクルで水素をヘリウムに変換
- 星はこの状態が最も安定
- 一生の大半を主系列星として過ごす
- 星の質量に応じてHR図上の位置が決まる
- 個々の星はHR図上で(ほぼ)同じ位置に留まる
主「系列」星と呼ばれる理由
- 以前(1930年頃まで)
星が高温 \(\to\) 低温に向けて進化すると考えられており、その名残で“main sequence stars”と呼ばれる- ただし1つの星団のHR図を考える場合あながち間違いではない(後述)
- 高温(大質量)の星:
早期型星(early-type stars) - 低温(低質量)の星:
晩期型星(late-type stars)
星の晩年1
赤色巨星 (red giant)
太陽の年齢と寿命(再掲)
- 横軸: 半径(太陽半径で規格化)
- 縦軸: 水素の重量比
- 各線は 10 億年毎 (0-100 億年)
現在の太陽中心部のH存在比は\(0.33\)と推測される。
\(\to\) 現在の太陽年齢は約46億年
太陽の寿命は約100億年
HR図上での“進化”
- 中心部で水素が枯渇
- He \(\to\) C \(\to \cdots\) の順に燃焼が進む
- どこまで燃焼が進むかは星の質量に拠る
- HR図上の位置で星の質量や進化段階を特定出来る
主系列後の進化1:赤色巨星
- 中心部で水素が枯渇
- ヘリウムコアの生成
- ヘリウムが核融合を起こすには圧力が不足
- 中心部は収縮 \(\to\) 密度上昇
- 中心部の外側で水素核融合
- “shell burning”
- 圧力上昇\(\to\)星全体は膨張
- 表面温度が下がり
「赤色巨星」(red giant stars)となる
HR図上の赤色巨星の“進化”
- 主系列の位置から右上に「赤色巨星分枝」(red giant branch: RGB) を進む
- ヘリウム核が大きくなるに従い加速度的に進む
- \(1~M_{\odot}\)の星はRGB上に5億年程度滞在
太陽の場合
最大半径は\(>100 R_{\odot}\)
質量放出
- 巨星は膨れ上がった表面からガスが流れ出す
- 質量放出: mass loss
- 星間塵の供給源のひとつ
- 赤色巨星の場合、典型的な質量放出率は小さい
- \(< 10^{-8} ~\mathrm{M}_{\odot}~\mathrm{yr}^{-1}\)
- cf. 太陽風による質量放出率 \(\sim 10^{-14} ~\mathrm{M}_{\odot}~\mathrm{yr}^{-1}\)
- slow wind: \(v_{\mathrm {wind}} \simeq 5–30~\mathrm{km~s^{−1}}\)
- \(1 M_{\odot}\) の星の場合、赤色巨星の間に \(0.25 M_{\odot}\) 程度の質量を失う
- 但し質量放出の正確な原因は不明
- 恐らくは太陽風と同様の磁場駆動か輻射圧による
低質量星の終末 \(( M < 0.5 M_{\odot} )\)
- 水素の核融合には\(T\geq 10^7\)Kが必要
- ヘリウムの核融合には\(T\geq 10^8\)Kが必要
- \(M < 0.5 M_{\odot}\) の星の場合、赤色巨星段階でもヘリウムの核融合が始まらない
- 水素の殻燃焼終了後星は冷えて一生を終える
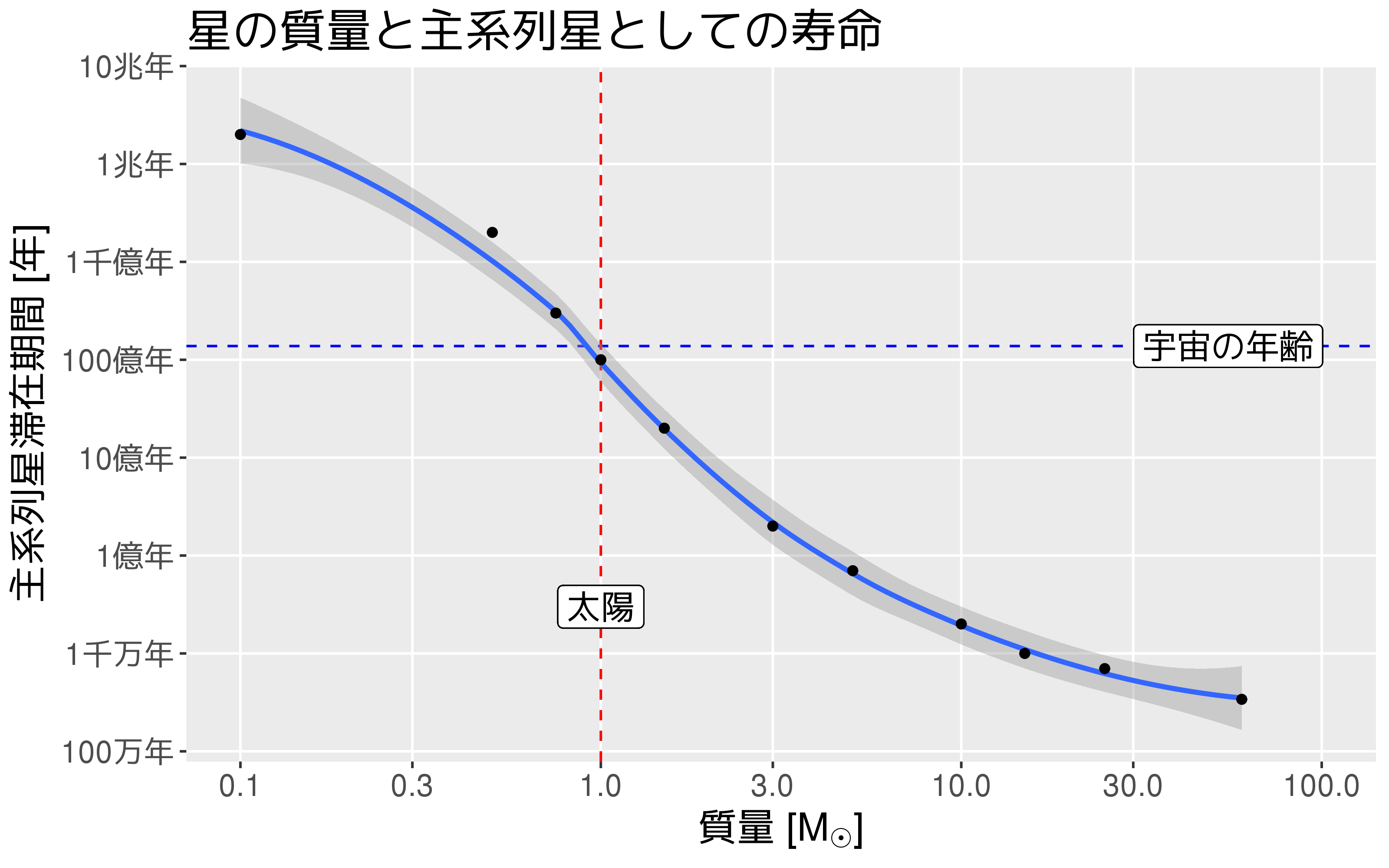
ただし低質量星の寿命は
宇宙の年齢よりも長い
ことに注意
星の晩年2
ヘリウム核燃焼
“トリプル\(\alpha\)”反応
- \(T > 1-2 \times 10^8\) K で開始
- 3つのヘリウム原子核(“\(\alpha\)粒子”)からひとつの炭素原子核を作る反応
- 原子核反応の際に観測される放射線を\(\alpha\)線,\(\beta\)線,\(\gamma\)線と命名
- \(\alpha\)線:ヘリウム原子核
- \(\beta\)線:電子
- \(\gamma\)線:高エネルギーの光子
- 原子核反応の際に観測される放射線を\(\alpha\)線,\(\beta\)線,\(\gamma\)線と命名
- 先ず2体反応で\(^8\mathrm{Be}\)を生成
- \(^8\mathrm{Be}\)は不安定同位体
(寿命\(10^{-16}\)秒)
- \(^8\mathrm{Be}\)は不安定同位体
- もう一つのヘリウムと反応して\(^{12}\mathrm{C}\)を生成
Triple-alpha process
\[\begin{align} \mathrm{He} + \mathrm{He} &\to \mathrm{Be}\\ \mathrm{Be} + \mathrm{He} &\to \mathrm{C} + \gamma \end{align}\]ファウラー (1911–1995): この過程の存在を実験的に証明し 1983年ノーベル物理学賞受賞
水平分枝 (Horizontal Branch)
- 中心核ではヘリウム、その外側では水素が核融合
- 中心核の膨張により、水素の燃焼殻も膨張\(\to\)反応率は低下
- 星の表面温度は上がるが半径は縮小\(\to\)HR図上を左に進む
- \(1~M_{\odot}\)の星はHB上に1億2千万年程度滞在
距離指標としての水平分枝
- ヘリウム核の燃焼はヘリウム核質量\(0.46~M_{\odot}\)で開始
- 星全体の質量に依らない
- HBの星の明るさは低質量星\((\leq 1.4~M_{\odot})\)の場合どの星もだいたい同じ\(\sim 50~L_{\odot}\)
- 距離指標 (standard candle)として用いることが出来る
- 星団の星はほぼ同時に生まれたと考えられる\(\to\)HR図から年齢が決められる
星の晩年3
赤色超巨星 (red supergiant)
ヘリウム核燃焼の終了
- 中心核には炭素が溜まる
- ヘリウム核融合の終了
- \(3\alpha\)反応で得られるエネルギーはCNOサイクルの\(<1/10\)以下
- ヘリウム核燃焼は水素核燃焼の1/100程度の期間で終了
- 太陽質量の星なら1億年程度
- 炭素核融合\(>5\times10^8\) Kが必要
- cf.ヘリウム\(>1\times10^8\) K
- \(<8~M_{\odot}\)の星は炭素核融合を開始出来ない
- 中心核の収縮により高温化\(\to\)ヘリウム殻燃焼の開始
漸近巨星分枝
- 水素殻燃焼(赤色巨星)と同様にHR図を右上に移動
- 巨星枝に“漸近”することから
「漸近巨星分枝」(Asymptotic Giant Branch: AGB)
と呼ばれる - \(1~M_{\odot}\)の星の明るさは\(L\sim 10^5L_{\odot}\)にも達する
- AGBの滞在期間は\(\sim500\)万年\((1~M_\odotの星の場合)\)
AGB星の変光
- AGB星のエネルギー源:水素とヘリウムの殻燃焼
- ヘリウム殻燃焼により外側の水素殻燃焼を抑制
- ヘリウム殻が燃え尽きると水素殻燃焼によりヘリウム供給
- ヘリウム殻と水素殻が交互に燃焼
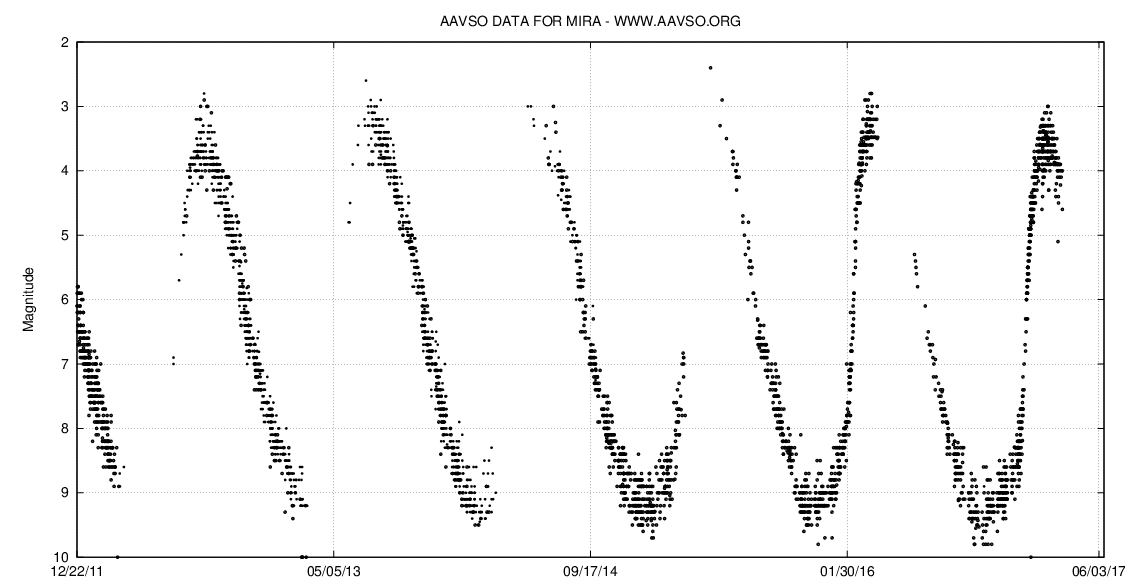
\(\to\)星全体が“脈動変光”を起こす - 代表例はくじら座のミラ
- 「ミラ型変光星」と呼ばれる
ミラの変光光度曲線

脈動に伴う質量放出
- AGB星は脈動に伴い外層から多くの質量を放出
- \(10^{-8}-10^{-4} ~\mathrm{M}_{\odot}~\mathrm{yr}^{-1}\) (右図参照)
- cf. RGB星の質量放出率は\(< 10^{-8} ~\mathrm{M}_{\odot}~\mathrm{yr}^{-1}\)
- AGB滞在中に水素の外殻の大半を放出
- AGBの滞在期間は\(100 \sim 200\)万年程度
- 質量放出率で決まる
質量放出の総量
MiraのALMAによる観測画像
ミラの星風によるtail
LL Pegasi (伴星を持つミラ型変光星)
LL Pegasi の3次元構造モデル
惑星状星雲
AGB周囲の星雲
- AGB星からの質量放出
- 水素の外殻の大半を放出
- 高温の中心核がむき出しになる
- 小質量の“矮星” (dwarfs/dwarf stars) が残る
- \(T_{eff} \sim 5 \times 10^4\)K \(\to\) “白色矮星”(white dwarfs)
- 周囲には吹き飛ばされたガス雲
- 中心星からの紫外線に照らされて輝く
- 昔の望遠鏡で一見惑星の様に見えたことから“惑星状星雲”(planetary nebulae)と呼ばれる
- 白色矮星中心部では核融合は止まっており、徐々に冷却して星の一生を終える
HTS images
星の一生のまとめ(太陽質量の星の場合)
太陽より重い星の進化
オリオン座の一等星
星内部の核融合プロセス
\(\geq 8\ \mathrm{M}_{\odot}\)の星は炭素核融合が可能
Heより重たい元素の燃焼: \(\alpha\)プロセスの進行
Triple-alpha process
\[\begin{align} \mathrm{He} + \mathrm{He} &\to \mathrm{Be} + \gamma\\ \mathrm{Be} + \mathrm{He} &\to \mathrm{C} + \gamma \end{align}\]Alpha process
\[\mathrm{^{12}C} + \mathrm{^4He} \to \mathrm{^{16}O} + \gamma\] \[\mathrm{^{16}O} + \mathrm{^4He} \to \mathrm{^{20}Ne} + \gamma\] \[\mathrm{^{20}Ne} + \mathrm{^4He} \to \mathrm{^{24}Mg} + \gamma\] \[\mathrm{^{24}Mg} + \mathrm{^4He} \to \mathrm{^{28}Si} + \gamma\] \[\mathrm{^{28}Si} + \mathrm{^4He} \to \mathrm{^{32}S} + \gamma\] \[\mathrm{^{32}S} + \mathrm{^4He} \to \mathrm{^{36}Ar} + \gamma\] \[\mathrm{^{36}Ar} + \mathrm{^4He} \to \mathrm{^{40}Ca} + \gamma\] \[\mathrm{^{40}Ca} + \mathrm{^4He} \to \mathrm{^{44}Ti} + \gamma\] \[\mathrm{^{44}Ti} + \mathrm{^4He} \to \mathrm{^{48}Cr} + \gamma\] \[\mathrm{^{48}Cr} + \mathrm{^4He} \to \mathrm{^{52}Fe} + \gamma\] \[\mathrm{^{52}Fe} + \mathrm{^4He} \to \mathrm{^{56}Ni} + \gamma\]
巨星の内部構造
セファイド型変光星 (Cepheids)
セファイド型変光星の周期-光度関係
- 光度 \(300 \sim 25000\ L_{\odot}\)
- 変光周期 \(1日 \sim 50日\) (最長250日)
- 変光周期から星の明るさが分かる \(\to\) 距離測定に使える
変光の理由:星内部のガスによる光の吸収
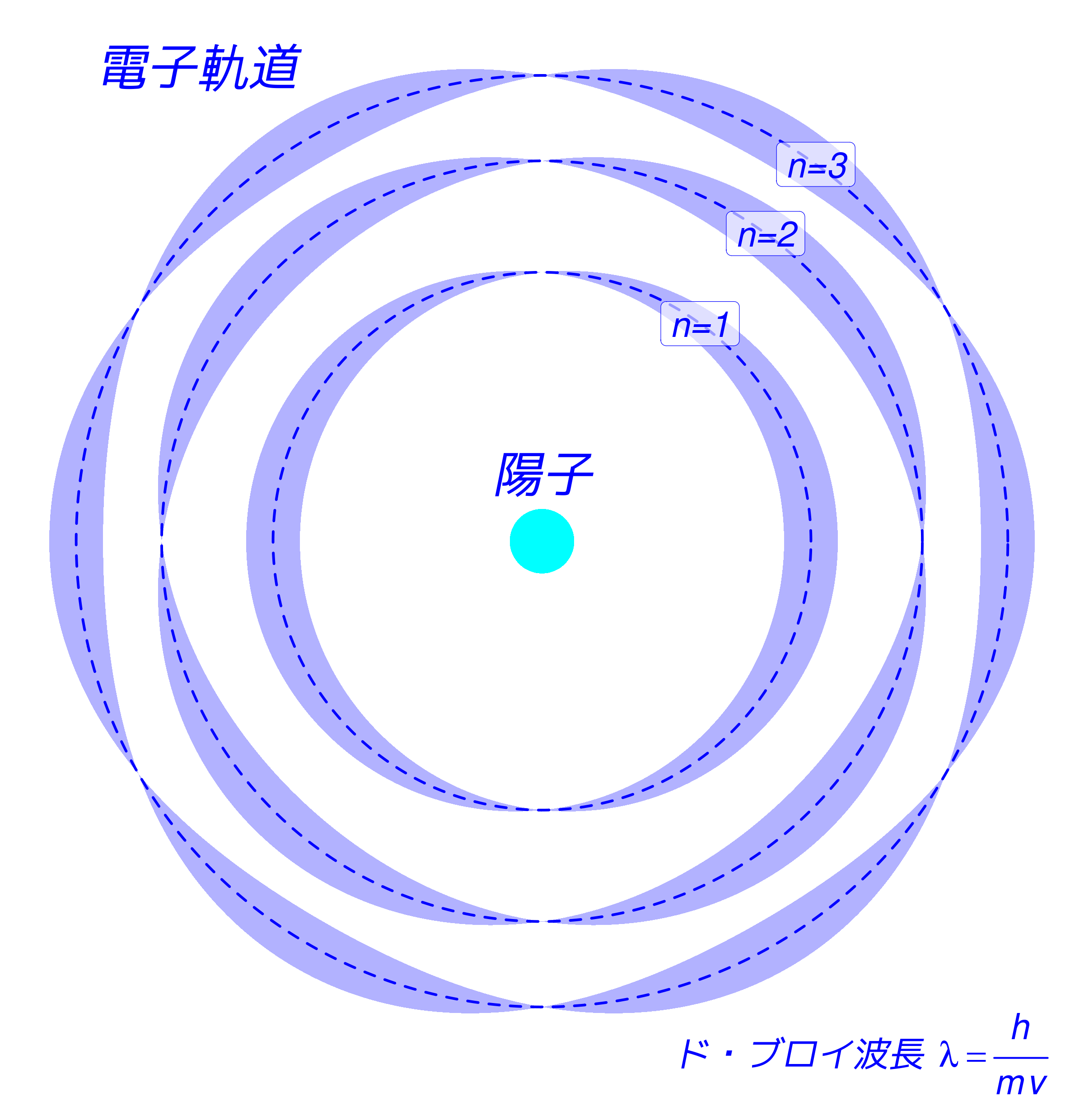
水素“原子模型”
(Bohr model)
エネルギー準位と吸収線
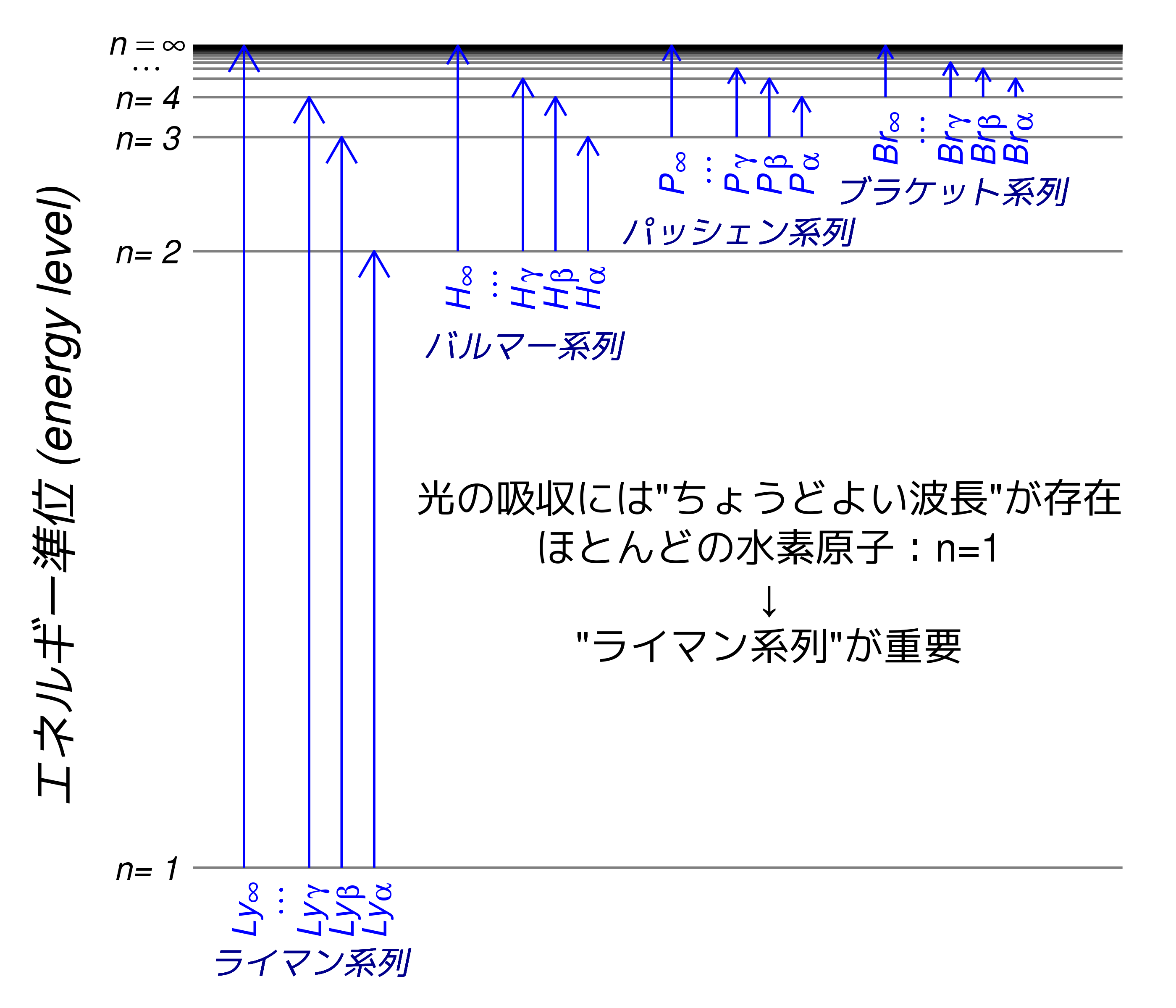
水素スペクトル吸収線
温度が1万度を超えると急激に吸収係数が増大
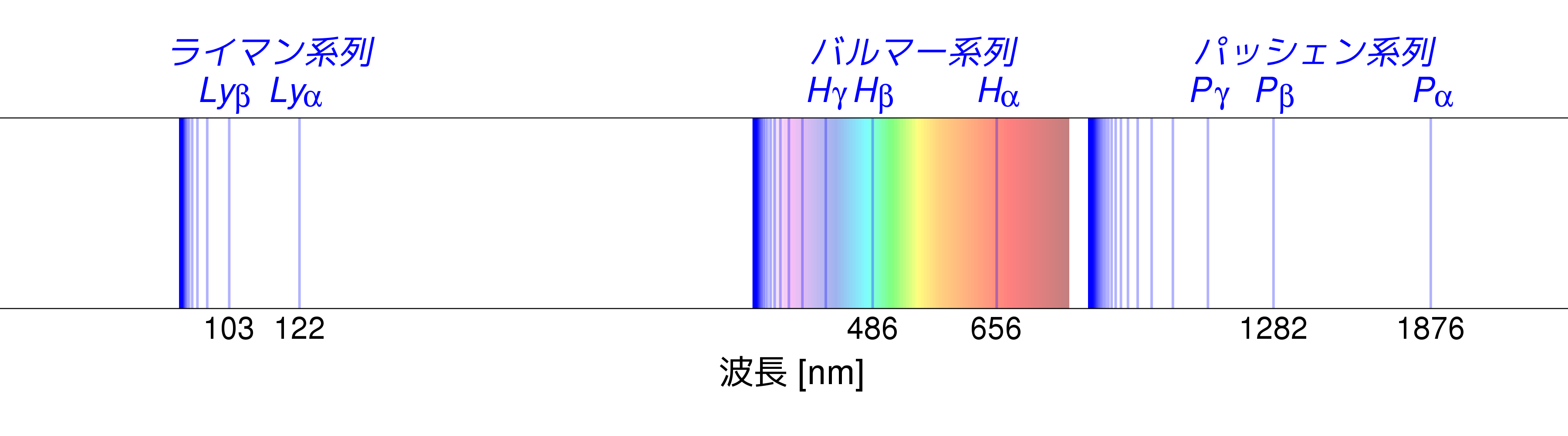
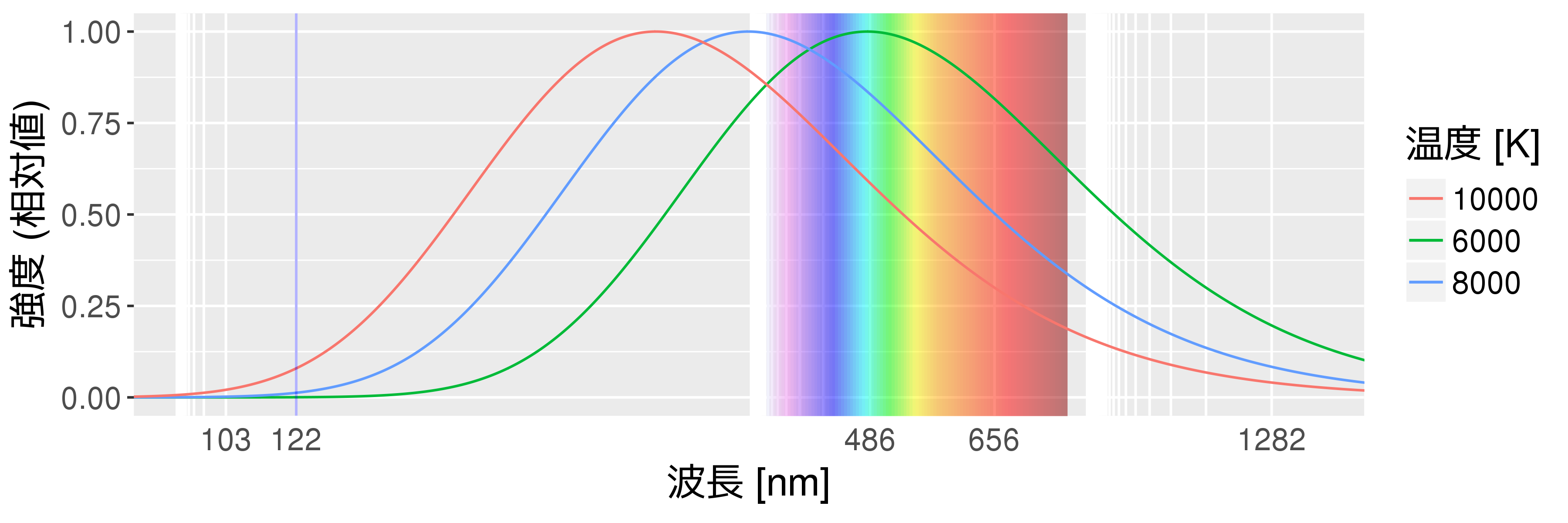
ガスの光吸収係数の温度依存性
- ガス温度は不安定領域に留まれない
- 温度上昇 \(\to\) 吸収係数大 \(\to\) 温度更に上昇
- 温度下降 \(\to\) 吸収係数小 \(\to\) 温度更に下降
- 不安定領域の前後で温度\((= ガス圧)\)が振動
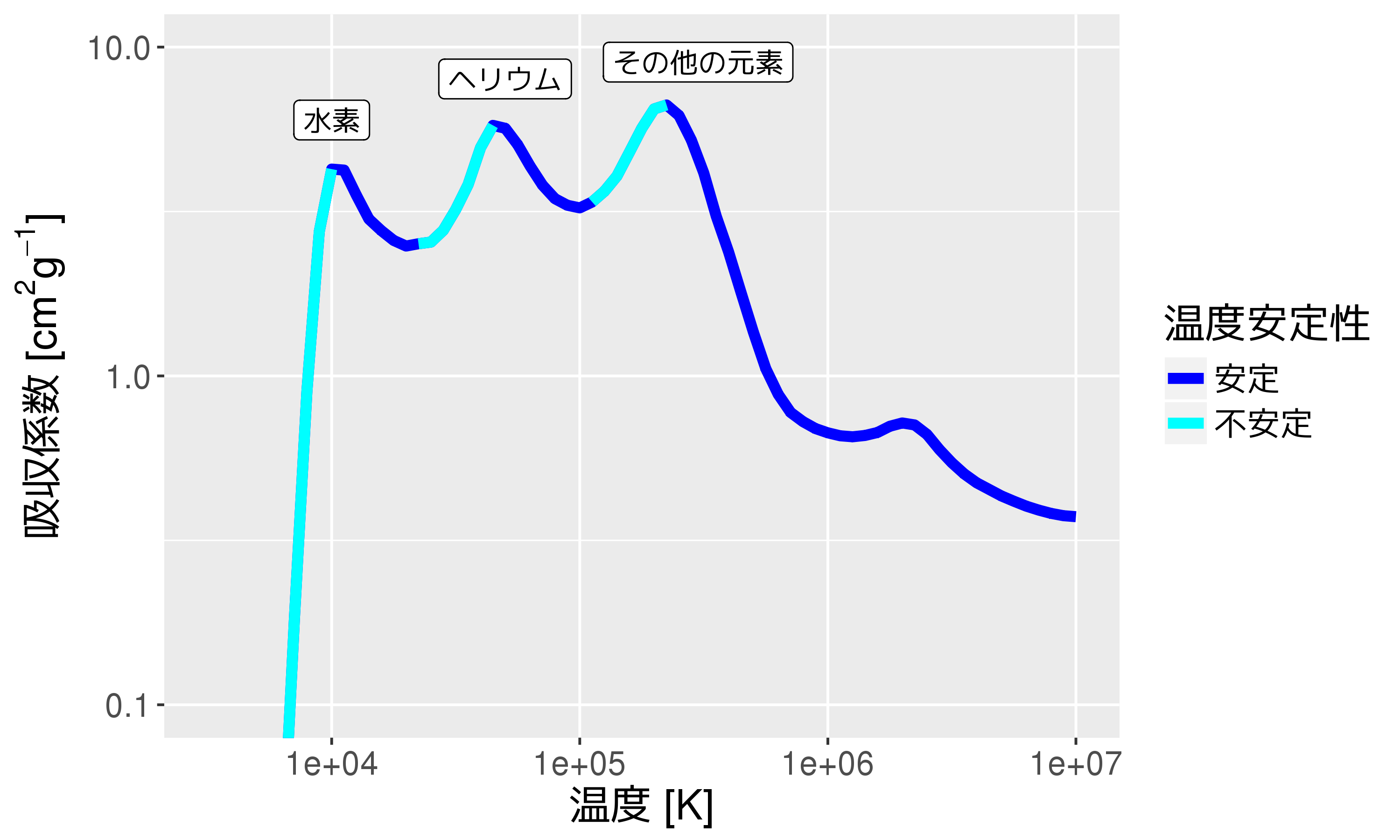
Seaton, Yan, Mihalas, & Pradhan 1994, MNRAS, 266, 805 よりおおよそ\(10~\mathrm{M}_{\odot}\)の星に相当する計算値を引用。
変光の原因:“脈動”の励起
- 特定の温度で不安定 \(\to\) ある深さに不安定層が存在
- 不安定層の振動が星表面の脈動を励起出来る条件
- 不安定層により押し広げられる外側のガス量
- 表面温度低 \(\to\) 不安定層が内側 \(\to\) ガス量多
- 表面温度高 \(\to\) 不安定層が外側 \(\to\) ガス量少
- 振動の周期が外側のガスの振動とマッチ(共振)
- 不安定層により押し広げられる外側のガス量
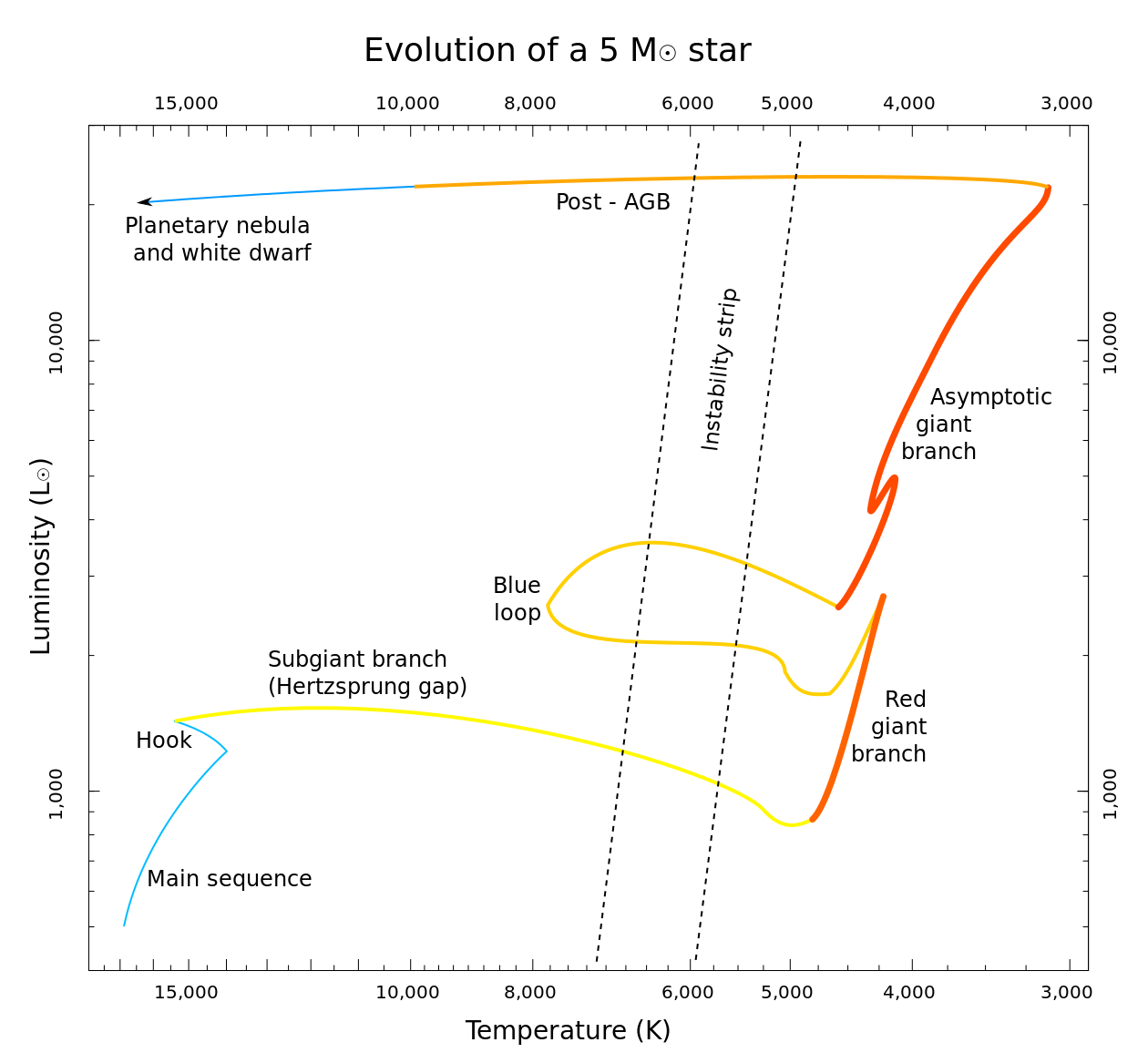

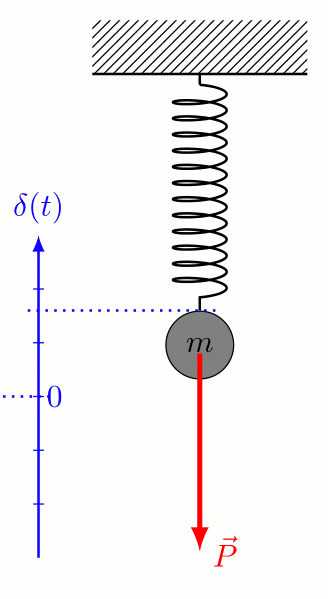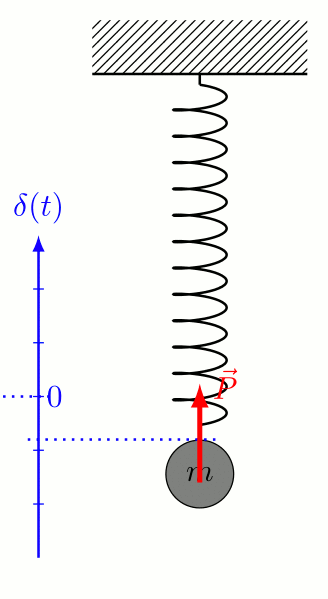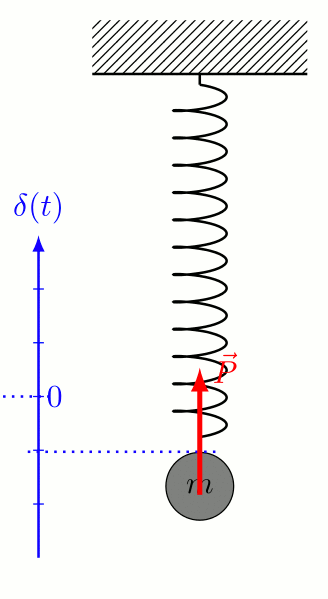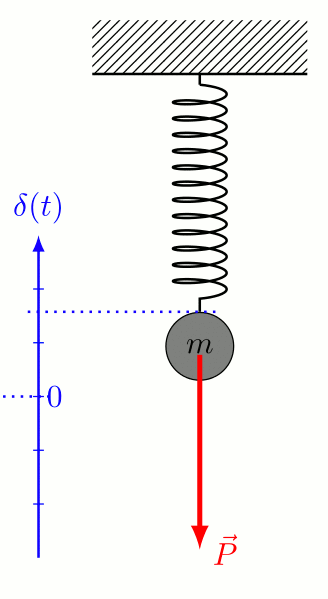
周期-光度関係の理由
| 項目 | 小質量星 | 大質量星 |
|---|---|---|
| 星質量 | 小 | 大 |
| 直径 | 小 | 大 |
| 光度 | 暗い | 明るい |
| 密度 | 高(硬い) | 低(軟らかい) |
| 振動周期 | 短い | 長い |
Leavittによる周期-光度関係の発見
- Henrietta Swan Leavitt (1868–1921)
- 小マゼラン星雲の1777個の変光星を観測
- 25個の変光星で周期-光度関係を発見

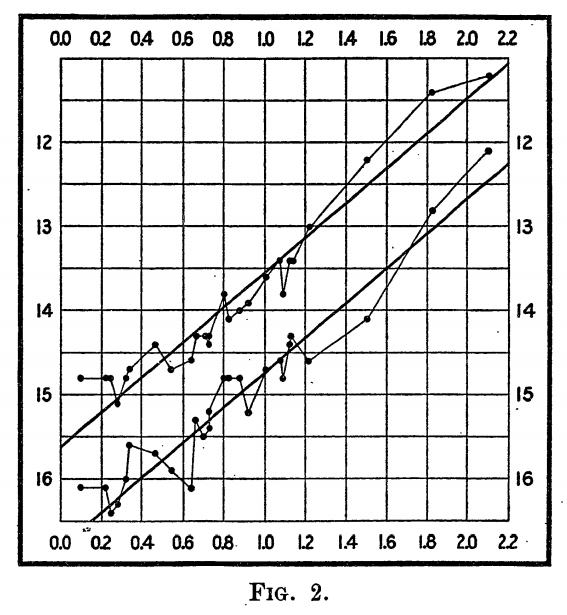
左図:Henrietta Swan Leavitt (1868–1921) (Wikimedia commons)
右図:彼女の発見した周期-光度関係 (Leavitt, & Pickering 1912, Harvard College Observatory Circular, 173, 1)
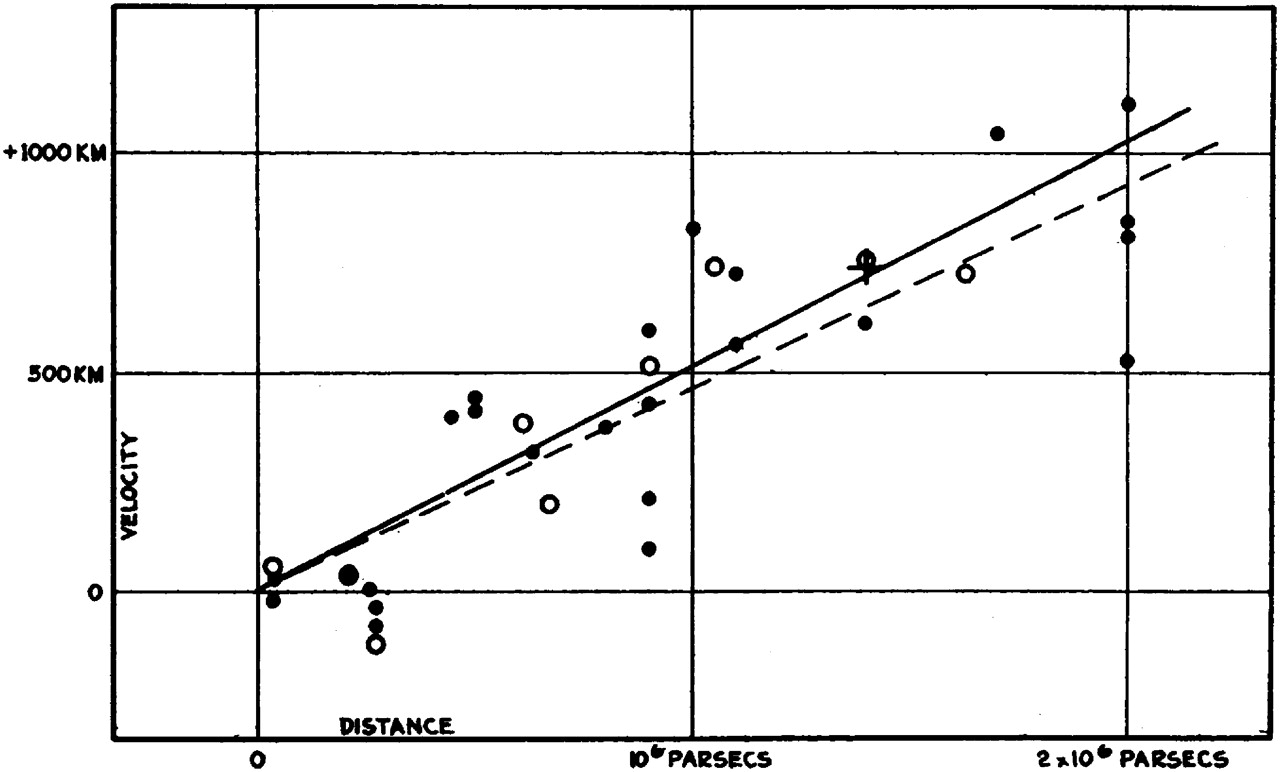
Hubble による応用
- “星雲”が遠く離れた銀河であることを確定(1924)
- 宇宙膨張の発見(1929)
横軸はセファイドから求めた距離: \(10^6\), \(2\times 10^6\) pc \(= 326万,~652万光年\)
超新星爆発
(重力崩壊型)
元素の束縛エネルギー (nuclear binding energy)
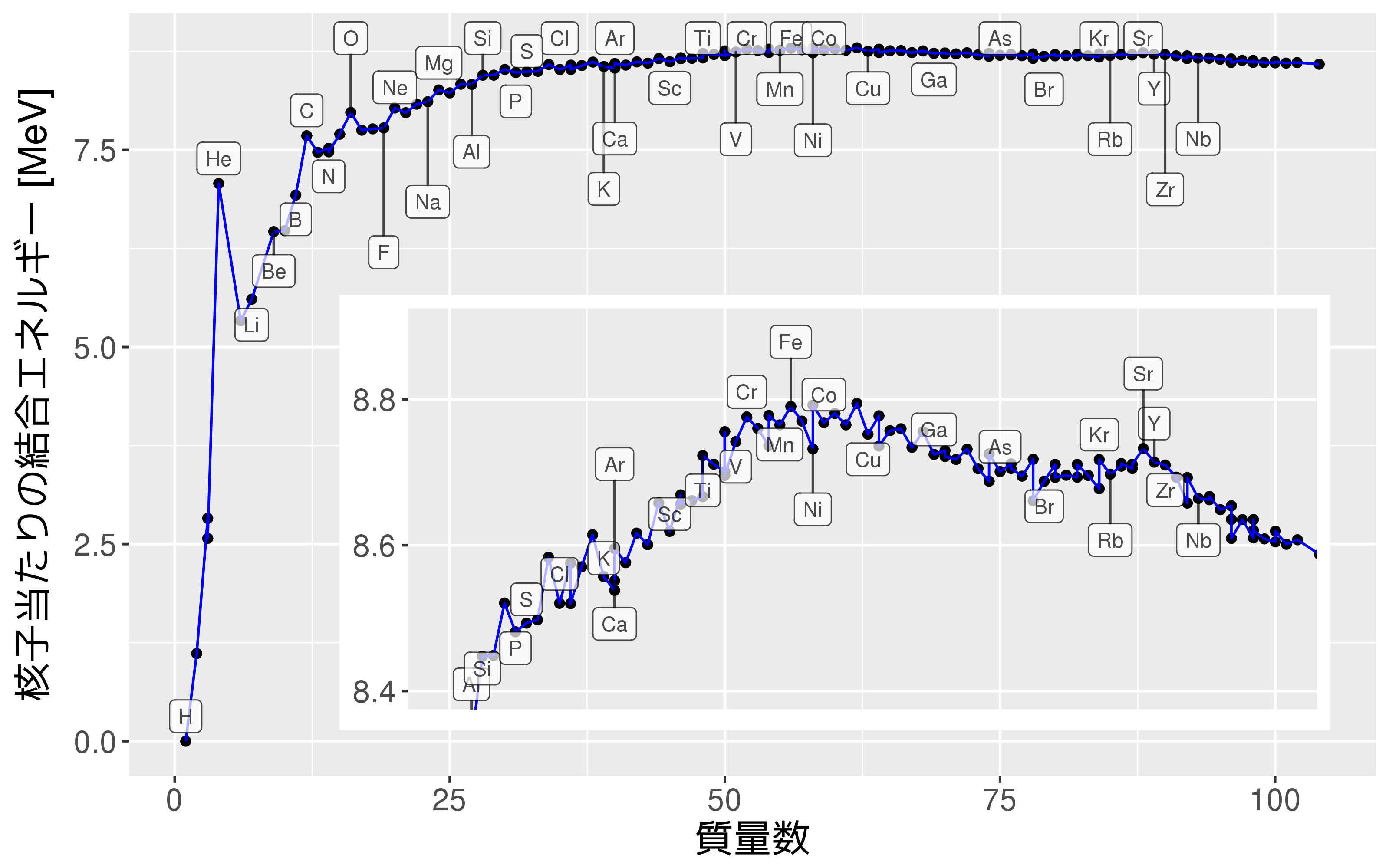
星の中心核の重力崩壊 (core collapse)
- 核融合で生成出来るのは鉄まで
- 中心部で鉄が出来ると核融合がストップ
- エネルギーを生み出せず中心核は収縮
- 外側では鉄の生成が続き中心核質量増大
- \(> 10\ \mathrm{M}_{\odot}\)の星: 中心核の温度が100億度に達し、高エネルギーの光子により鉄が光分解
- \(8 \sim 10\ \mathrm{M}_{\odot}\)の星: チャンドラセカール限界\((\simeq 1.44\ \mathrm{M}_{\odot})\)を超える
- 電子が陽子に叩き込まれて中性子に
- 電子捕獲:\(p + e^- \to n + \nu_e\)
- (チャンドラセカールは1983年ノーベル物理学賞受賞)
- 中心核が一挙に潰れ、発生したニュートリノの急激な加熱により星全体が爆発\(\to\)超新星爆発
重力崩壊型超新星爆発
Type II SNe (super novae)
超新星爆発ニュートリノ
- 1987年2月23日に発生
- 距離 50 kpc (16.3万光年)
- 近傍銀河での超新星は400年ぶり
- 感度向上した“Kamiokande-II”が1ヶ月前に観測開始直後
- 小柴先生退官2ヶ月前
- 2002年ノーベル物理学賞受賞
超新星爆発残骸
(Supernova Remnant; SNR)
かに星雲の爆発イメージ
かに星雲 (Crab Nebula)
かに星雲の記録
藤原定家による「明月記」寛喜二年十一月八日(1230年12月6日)の日記に陰陽師安倍泰俊の報告を挿入。
超新星の古記録
Wikipedia- SN185 (宋書)
- SN393 (後漢書)
- SN1572 (ティコの星)
- SN1604 (ケプラーの星)
1604年以降銀河系内では超新星は観測されていない
ティコの星 (Tycho’s SNR)
中性子星
中性子星の予測
- 超新星爆発により中心に中性子星が出来る
- \(\geq 30~\mathrm{M_{\odot}}\)の星ではブラックホールが出来る
- チャンドラセカール限界を越えた白色矮星の崩壊
- 連星系の伴星からの質量降着
- 1934年 Baade & Zwicky により存在が予測
- 半径10km程度\(\to\)暗く発見が困難
“パルサー”の発見
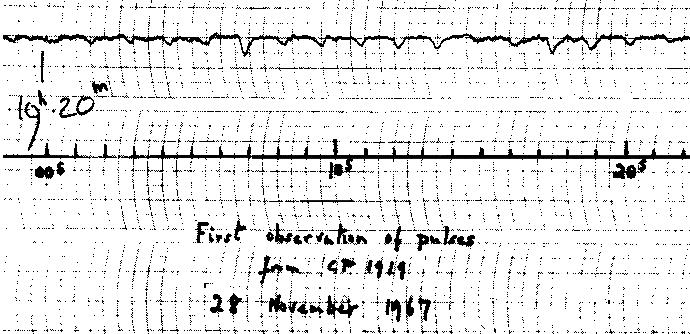

- 1.3秒間隔の規則的な電波パルス
- Jocelyn Bell (ケンブリッジ大学院生) により観測 (1967)
- 指導教員の Antony Hewish らと共に論文発表
- Hewish は 1974 にノーベル物理学賞受賞
パルサー
- 強い磁場を持つ天体が高速回転
- 磁場による電子の加速により
極方向に強い電波を発する - ただし当初は正体不明
- 地球外生命体も最初疑われる
中性子星
- かにパルサー(周期33msec: ミリ秒パルサー)の発見(1968)
- \(遠心力 \leq 重力\)の条件から星に許される半径を見積もる
より、\(M = 1\ \mathrm{M}_{\odot}\) なら \(r \leq 154\) km
\(\Rightarrow\) 白色矮星(\(M \simeq 1\ \mathrm{M}_{\odot},\ r \simeq 10^{3-4}\) km)ではあり得ず
中性子星であることが確定
Ia型超新星
(Type Ia SNe)
白色矮星
- \(<8~M_{\odot}\)の星は炭素核融合を開始出来ない
- 外層は流出し惑星状星雲に
- 中心部に\(\sim 1\ \mathrm{M}_{\odot}\)の“芯”が残る
- 中心部は炭素・酸素に富む
- “電子縮退圧”により支えられる
- 原子同士が“くっつきあった”状態
- チャンドラセカール限界(\(1.44\ \mathrm{M}_{\odot}\))を超えると
電子が原子核に叩き込まれて一挙に崩壊
- 縮退圧で支えられたガスは、密度が温度に拠らない
- 通常のガス:温度上昇 \(\to\) 膨張して密度低下
- 縮退したガス:温度上昇しても密度変わらず
- 縮退したガス中の核融合:密度が変わらないまま温度上昇し、核融合反応が暴走
Type Ia SNe
- 白色矮星と通常の星の連星(白色矮星同士の連星との説も)
- 白色矮星表面への質量降着
- 降着したガスが白色矮星の表面で間欠的に水素核融合
新星(Novae) - 爆発毎に降着質量の40%以上が積もる
- \(1.38\ \mathrm{M}_{\odot}\)中心部の炭素が核融合開始 \(\to\) 暴走し爆発
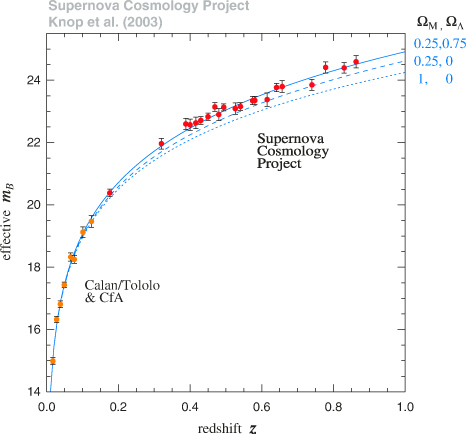
距離指標としての Type Ia SNe
- 爆発時の質量一定 \(\to\) 爆発の明るさが一定
- 距離指標として利用可能
- 輝度が高く、遠方の距離測定に使える

ブラックホール
中性子星の崩壊
- 中性子星質量が\(\simeq 2\ \mathrm{M}_{\odot}\)を超えると中性子自身の縮退圧でも支えられなくなる
- ブラックホールに崩壊
- 質量は\(\leq 10\ \mathrm{M}_{\odot}\)程度


ブラックホールの半径
質量 M の天体から距離 r にある質量 m の物体が無限遠に到達できる条件: \(運動エネルギー \geq 位置エネルギー\) \[\frac{1}{2}m v^2 \geq \frac{GMm}{r}\] 両者が等しい場合の速度を脱出速度と呼ぶ
\[ v_{esc} = \sqrt{\frac{2GM}{r}} \]
\(v_{esc} = c\) (光速)となる半径がブラックホールの大きさ\(\to\) Schwarzschild 半径
\[ r_g = \frac{2GM}{c^2} \]
星の質量による進化のまとめ
星の質量による進化のまとめ
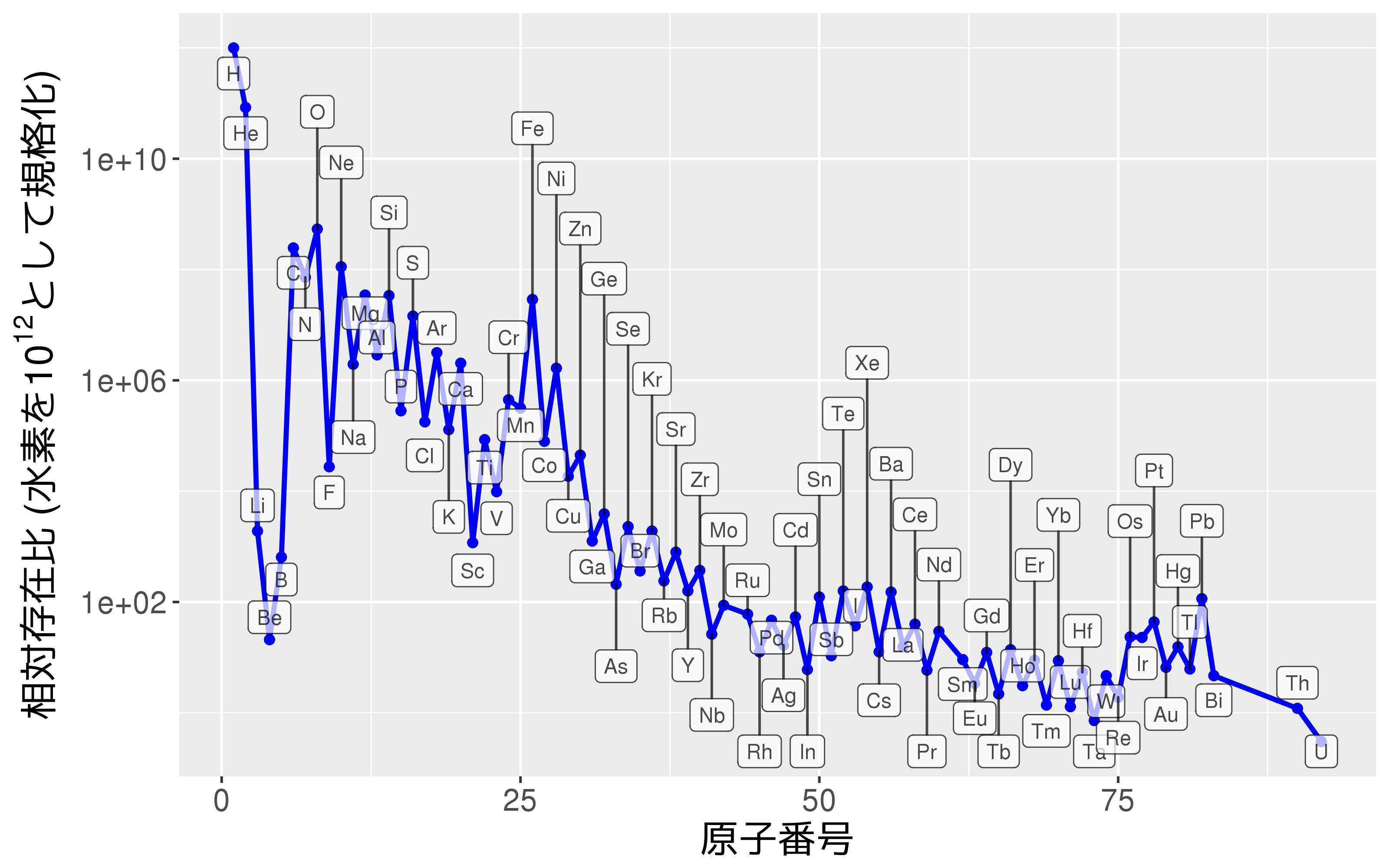
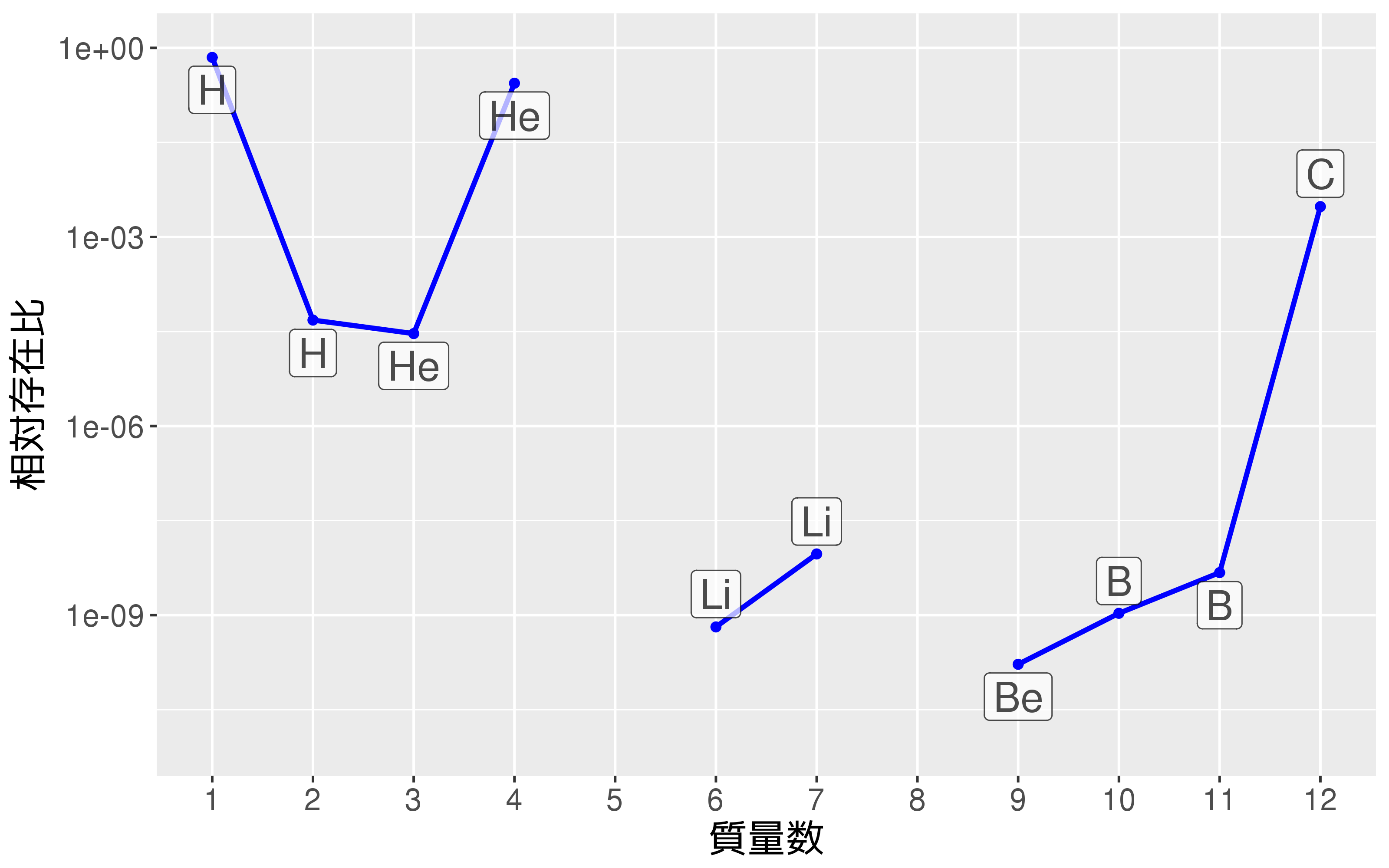
元素の生成
- 鉄(Fe)より重い元素は“r-process”により合成
生成物(太陽存在比)
重力波
重力波の観測法
レーザー干渉計
重力波の観測装置


LIGO : アメリカの2台のレーザー干渉計
重力波の検出
- 2015年9月14日9時50分45秒に重力波を初検出
- 質量\(35.4~\mathrm{M}_{\odot}\)と\(29.8~\mathrm{M}_{\odot}\)のブラックホールの衝突・合体
- 距離 410 Mpc (13億光年)
重力波の検出波形
Credit: Alex Nitz/Max Planck Institute for Gravitational Physics/LIGO
中性子星合体イベントの検出
中性子星合体の検出
Credit: Alex Nitz/Max Planck Institute for Gravitational Physics/LIGO
中性子星合体
Credit: Alex Nitz/Max Planck Institute for Gravitational Physics/LIGO
発生源の同定
発生源の同定
日本の望遠鏡群による追観測
中性子星合体のr-processによる重元素合成
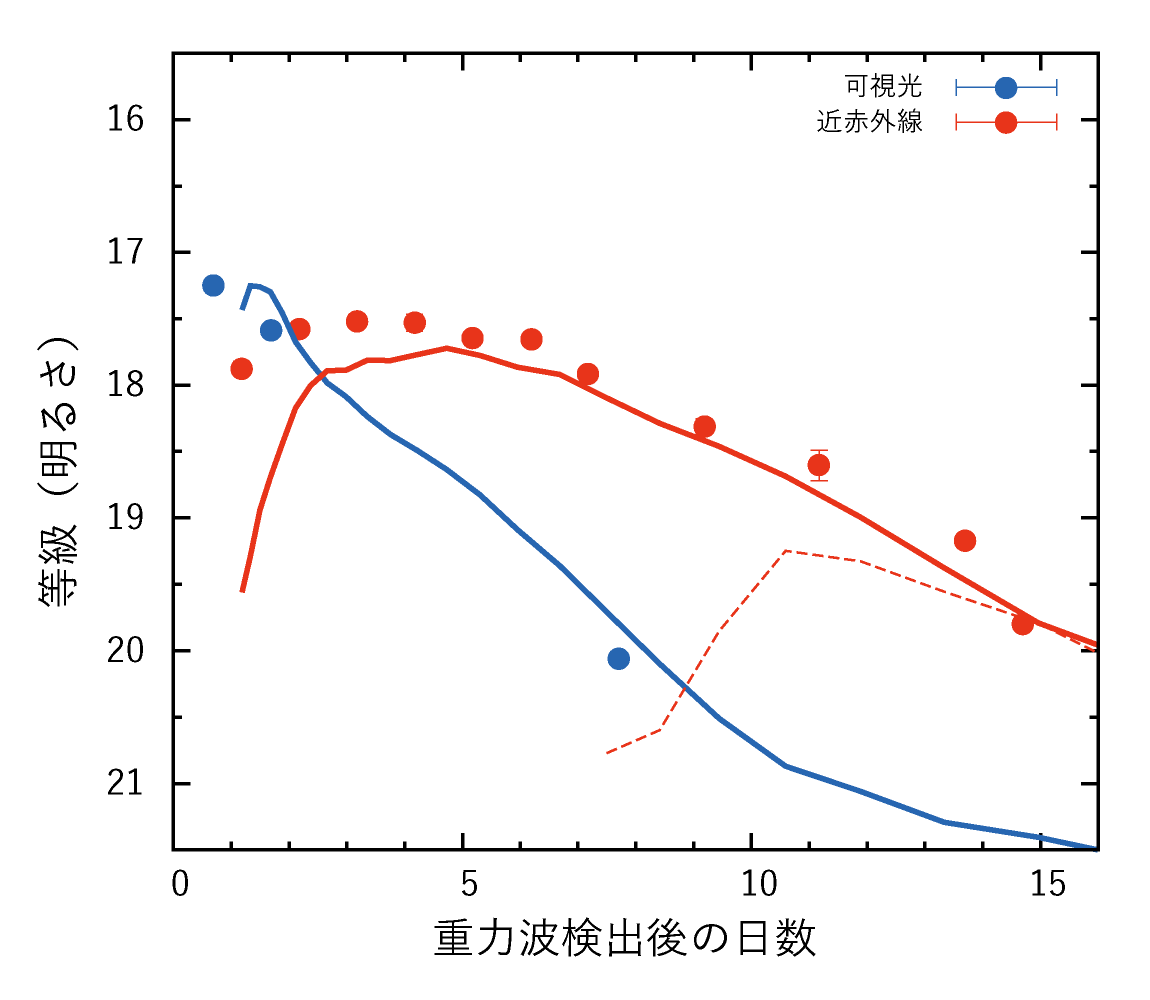
重力波源 GW170817 で実際に観測された明るさの変化 (●) と、シミュレーション (実線・破線) の比較。(クレジット: 国立天文台)
教科書が書き換わってしまった。
日本の重力波観測
TAMA300
1999年\(\sim\)
KAGRA
重力波の発見ラッシュ
It's been #AwesomeApril as the 1st month of #O3 produces 5 candidate #GravitationalWaves events! Are they merging #BlackHoles #NeutronStars or maybe even a #NS-BH first detection? @LIGO and @ego_virgo teams are chasing down the answers! (ps the @ehtelescope image was v cool too) pic.twitter.com/ZwyjG47MRZ
— LIGO (@LIGO) 2019年4月30日
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/Hertzsprung-Russel_StarData.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/jcd_fig2.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/bt2lf1612_a.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/hshellburningsml.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/e69_1.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/sunredginatcompsml.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/Triple-Alpha_Process.svg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/M5_colour_magnitude_diagram.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/carbonshellsml.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/AGB.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/aa23241-13-fig6.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/apj522470f8)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/potw1447a_asp.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/glx2007-04r_img03.jpg)


</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/howmuchdobin.jpeg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/Nucleosynthesis_in_a_star.gif)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/CepheidPL.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/plrelnceph.gif)


</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/tit_job_vol54_01.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/aat050a_25.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/shinsei_gazou02.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/3327_0_00.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/tumblr_om0696oxep1vjhboso1_500.gif)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/sn2006gy_newline.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/Nucleosynthesis_periodic_table.svg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/738px-GW170817_spectrograms.svg.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/apjlaa91c9f1.png)
](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/fig2j.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/tama_birds_view.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/kamioka_1.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/ObsScen_fig2_v11.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/img-main-visual.jpg)