宇宙科学I (文科生)
我々の銀河系
土井靖生
2019/12/20
今回のポイント
- 銀河系は「渦巻き銀河」
- 渦巻きの“腕”で星間ガスが圧縮され、星が生まれる
- 中心部には「大質量ブラックホール」が存在
- “銀河回転”の観測から銀河系の構造を推測
- “見えている物質”だけでは不足
\(\to\)“見えない物質”「ダークマター」の存在
- “見えている物質”だけでは不足
我々の銀河系
全天の星の分布
全天の星の分布
様々な波長で見た銀河系
(復習)
H\(\alpha\)
)</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/halpha.png)
A Full-Sky H\(\alpha\) Template for Microwave Foreground Prediction (Finkbeiner 2003, ApJS, 146, 407)
CO
)</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/co.png)
The Milky Way in Molecular Clouds: A New Complete CO Survey (Dame, Hartmann, & Thaddeus 2001, ApJ, 547, 792)
電波観測
)</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/Radio1.4GHz.png)
A New 1.4 GHz Radio Continuum Map of the Sky South of Declination \(+25^{\circ}\) (Calabretta, Staveley-Smith, & Barnes 2014, PASA, 31, e007)
赤外線全天画像
)</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/WideS.png)
The AKARI Far-Infrared All-Sky Survey Maps (Doi, Takita, Ootsubo, et al. 2015, PASJ, 67, 50)
HI全天画像
)</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/HI.png)
a full-sky HI survey based on EBHIS and GASS. (HI4PI collaboration 2016, A&Ap, 594, A116)
銀河系の形状
ハーシェルによる推定

“Section of our sidereal system.” Herschel, William. “On the Construction of the Heavens. By William Herschel, Esq. FRS.” Philosophical Transactions of the Royal Society of London 75 (1785)
- すべての星が同じ明るさとし、遠い星ほど暗く見えると仮定して距離を推定
- 直径約2kpc (約6000光年)、厚み約300pc (約1100光年)
現代の測定法:銀河回転の測定
CO 位置-速度図
CO 位置-速度図と銀河系構造との対応
銀河系全体図
各種天体の銀河系内の位置
暗黒物質 (dark matter)
銀河回転曲線

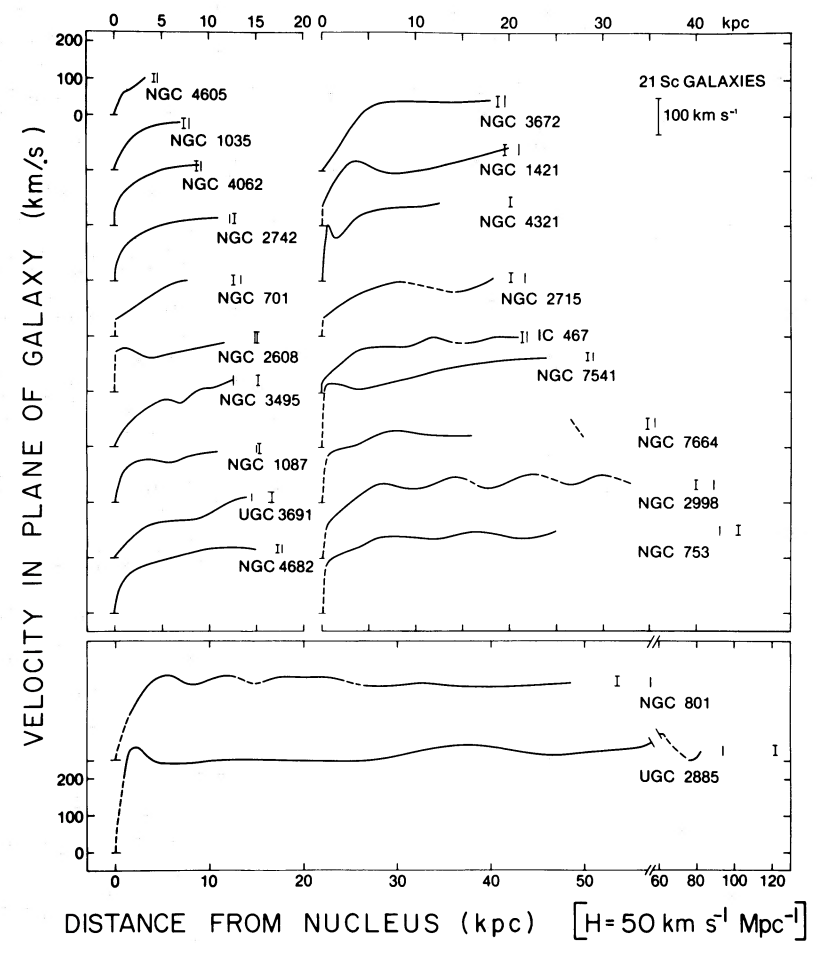
copyright: imgur
銀河回転とダークマター

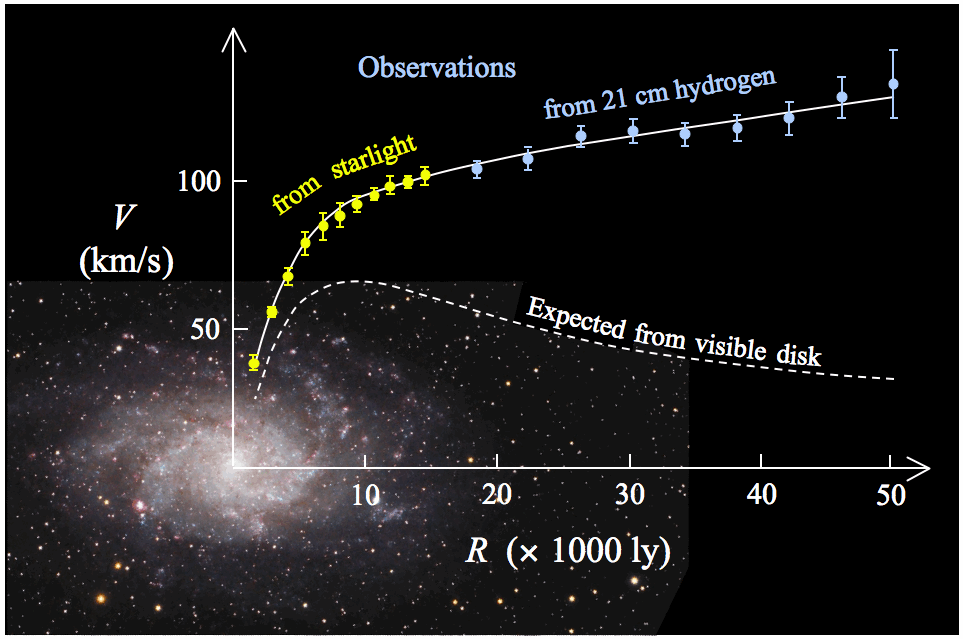
M31 (copyright: imgur)
M33 (copyright: Stefania.deluca via Wikimedia Commons)
- 遠方まで回転速度が落ちない
- 「見えない物質」が銀河の外側まで大量に分布していることを示す
- ダークマターの最初の直接的証拠(の1つ)
銀河系の構成
- 星の数: \(\sim 1-4\times 10^{11}\)
- 総質量: \(\sim 1.3\times 10^{12}\ \mathrm{M_\odot}\)
- 星の質量: \(\sim 5 - 6 \times 10^{10}\ \mathrm{M_\odot}\)
- ガスの質量は星の質量の\(\sim 1/10\)
- ほとんどの質量は「暗黒物質」が担う
- 星の輝度: \(\sim 1.5 - 2 \times 10^{10}\ \mathrm{L_\odot}\)
- 星形成率: \(\sim 1\ \mathrm{M_\odot ~ yr^{-1}}\)
- 太陽から銀河中心までの距離: \(\sim 8 - 8.5\) kpc
- 太陽系の公転速度: \(\sim 220\ \mathrm{km~s}^{-1}\)
- 銀河系を約2億年で一周
銀河系の構成要素
- 直径: \(\sim 50\) kpc
- 厚み: \(\sim 0.3 - 1\) kpc
- 比較的若い星、分子雲などから成る円盤
- 「種族Iの星」Population I stars と呼ばれる
- バルジ・ハロー
- 古い星、高温の星間ガスや暗黒物質が球状に分布
- 「種族IIの星」Population II stars と呼ばれる
- バルジ
- 輝度\(\sim 5\times 10^9\ \mathrm{L_\odot}\)
- 質量\(\sim 2\times 10^{10}\ \mathrm{M_\odot}\)
- ハロー
- 星質量\(\sim 10^9\ \mathrm{M_\odot}\)
- 数%の星が球状星団に属する
- 質量の90%はダークマターが担う
密度波による渦状腕の形成
渦状腕と分子雲
渦状腕に沿った分子雲の分布
ALMA望遠鏡の観測した濃い分子ガスの分布
可視光(ハッブル望遠鏡)と電波(ALMA)で見た渦状腕の比較
渦状腕による星間ガスの圧縮
- 渦状腕の内外で星間ガスの平均密度は3倍程度しか変わらない
- “濃いガス”の割合が大きく異なる(Torii et al., 2018)
- 平均値は\(2.9^{+2.1}_{-0.8}\%\)
- 腕の間では\(\sim 0.1 - 0.4\%\)
- 腕の内部は\(\sim 4 - 5\%\)
渦状腕に沿った星形成
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/eso1118a.jpg)
渦巻銀河 NGC 6744(ESO
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/AndromedaGalex_2048.jpg)
アンドロメダ銀河(Credit: GALEX, JPL-Caltech, NASA
星間ガス量と星形成率
星形成の効率
- ガスの量と星形成率に一定の関係
- Kennicutt-Schmidt law
- (普通の)銀河の平均的な星形成率は\(1\% - 数\%\)
\(\to\)星形成は非常に非効率 - ガスの圧縮が“たまたま”磁場に沿った方向に起こった場合に星形成に至るとする描像と良く合う
銀河中心
銀河中心付近の活動
- 多数の超新星残骸(SNR)や活発な星形成領域(Sgr B2)
- 銀河中心(Sgr A)からの強い電波輻射 \(\leftrightarrow\) 高い活動性
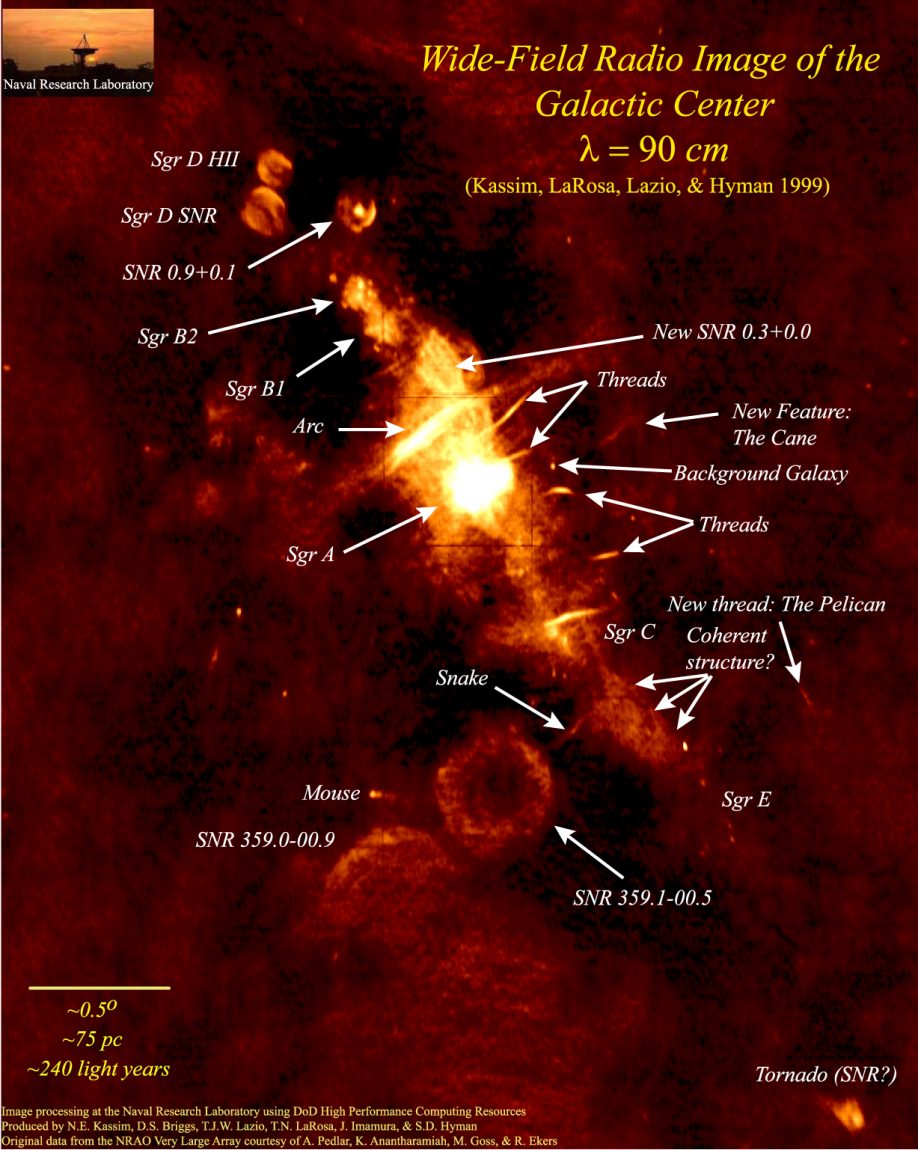

銀河中心拡大図
“mini-spiral”
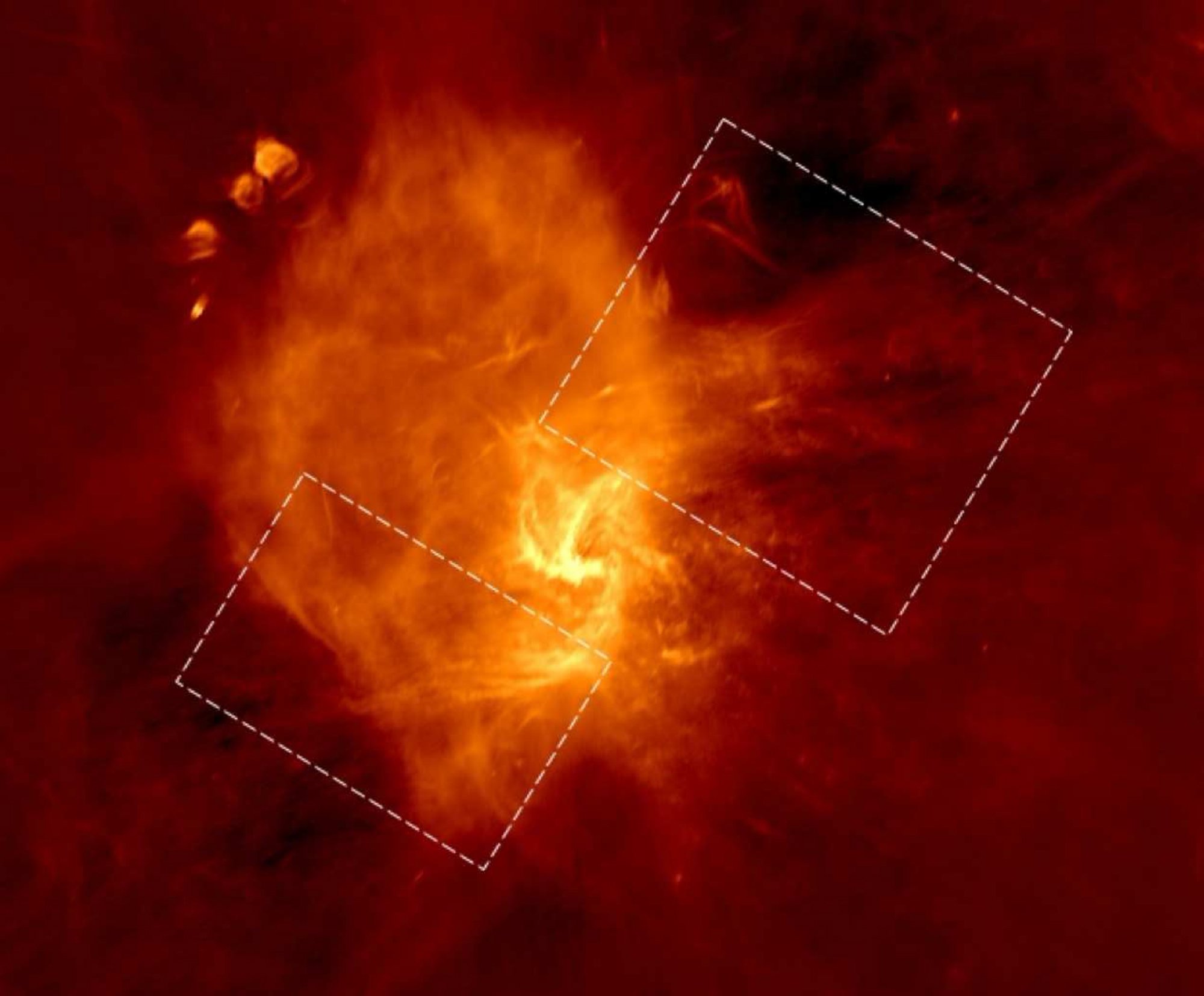

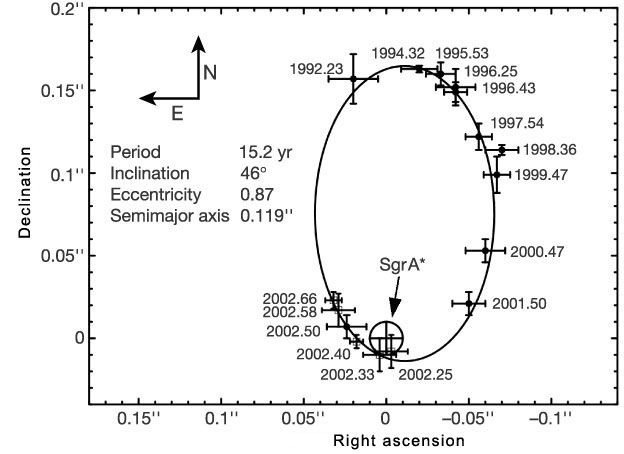
銀河中心付近の星の動き
中心付近を(無事)通過する星の動きから
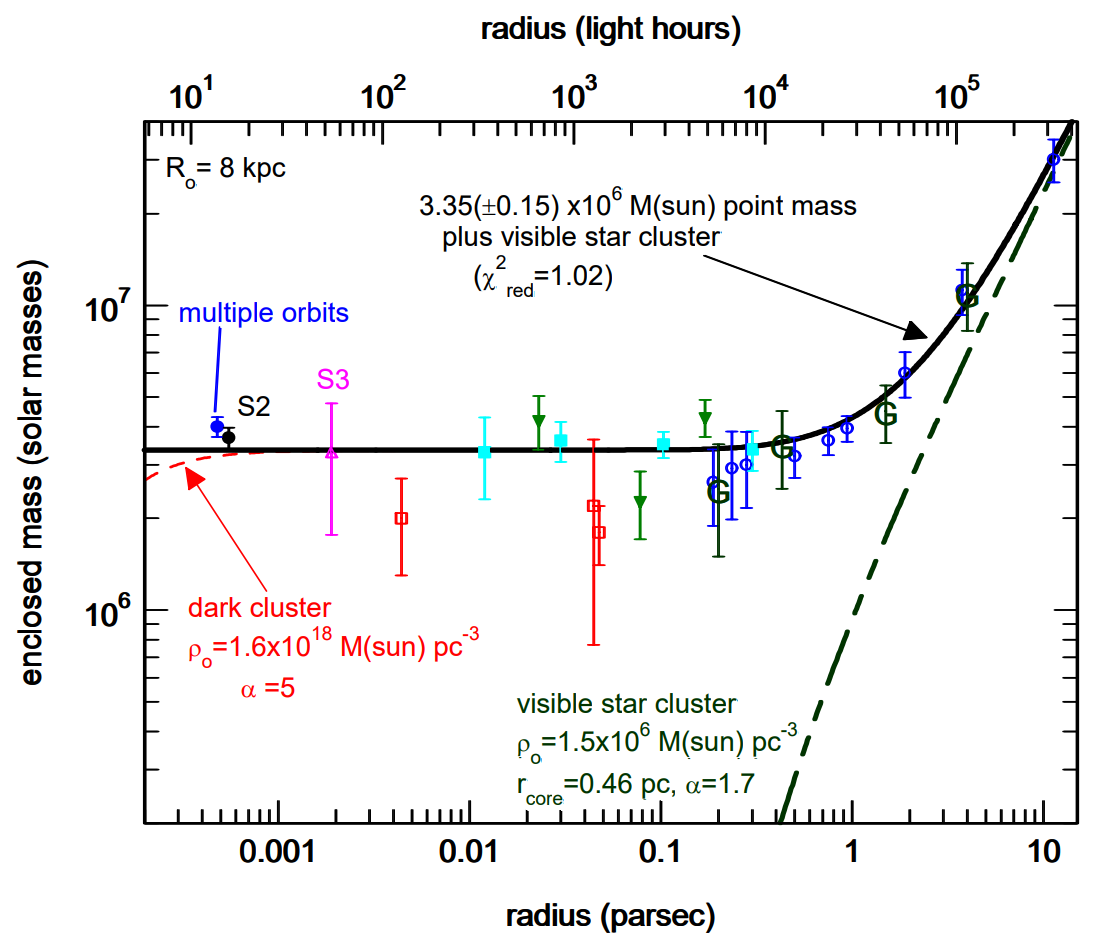
中心質量と最大半径を推定
大質量ブラックホール
中心質量の推定値: \((4.31 \pm 0.36) \times 10^6\ \mathrm{M_\odot}\ (R_0 = 8.33\ \mathrm{kpc}\))
銀河中心の活動性の源
降着円盤 (accretion disk)
解放される重力エネルギー
重力に引かれて半径\(r\)まで物を落とす際に
解放される位置エネルギー
\[ E = G\frac{Mm}{r} \]
\(r\)はシュバルツシルト半径 \(r_g=\frac{2GM}{c^2}\) より、\(E=\frac{mc^2}{2}\)
つまり、物質の持つエネルギーの最大50%を解放出来る!!
(実際には物をまっすぐ落とせない&吸い込まれる前にエネルギーを放射する必要あり、しかし\(10\sim40\)%のエネルギーを取り出せる)
(cf.水素核融合0.7%, 原子炉0.1%, 燃焼(酸化)\(10^{-10}\))
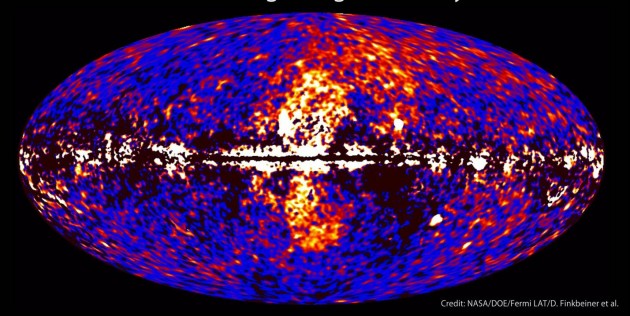
\(\gamma\)線
“Fermi bubble”

大質量ブラックホールの
直接観測
事象の地平線
ブラックホールの大きさ Schwarzschild 半径
\[ r_g = \frac{2GM}{c^2}\]
(\(M\)大ほど\(r_g\)大)
Schwarzschild 半径の内外では情報がやり取りできない \(\to\) “事象の地平線”
(event horizon)
Event Horizon Telescope
予想される銀河中心画像の直径は \(50\ \mu\mathrm{as}\)
超長基線電波干渉計 VLBI (very long baseline interferometer) ならば観測可能
EHTによる銀河中心画像(予想)
EHTにより実際に観測されたM87のBH画像
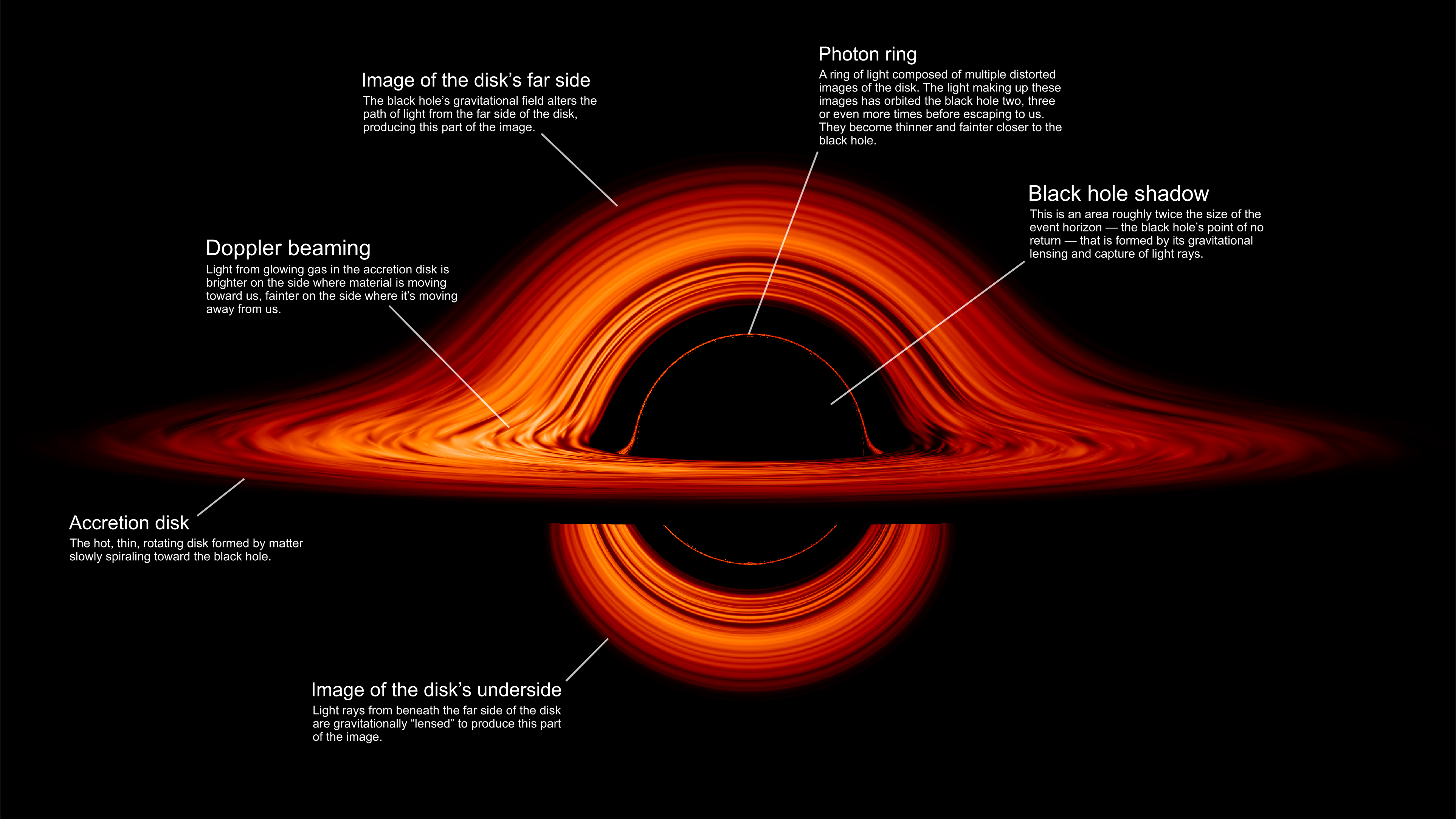
NASA によるブラックホールの
可視化シミュレーション

局部銀河群
LMC, SMC, M31の軌道
- 赤:アンドロメダ銀河
- 緑:大マゼラン銀河
- 黒:小マゼラン銀河
- 青:射手座矮小銀河
Magellanic stream
局部銀河群
アンドロメダ銀河との衝突合体
星と星との平均距離(銀河系の場合)
- 銀河系の星の数 \(\sim 10^{11}\)個
- 銀河系の体積 \(\sim \pi \times \left( 10\mathrm{kpc}\right)^2 \times 300 \mathrm{pc}\)
- 星の平均密度 \(\sim 0.94個/\mathrm{pc}^3\)
星と星との平均距離はおおよそ\(1\mathrm{pc}\)
銀河がすれ違う時の星の衝突確率
- \(1\mathrm{pc} = 2.1\times 10^{5} \mathrm{au}\)
- \(1\mathrm{pc}\) 走る毎に \(1\mathrm{pc}^2 = \left( 20万 \mathrm{au} \right)^2\)以内を星が1個通過
- \(100 \mathrm{au}\)以内を星が1回通過するためには\(\left( 20万 \mathrm{au} \right)^2 / \left( 100 \mathrm{au} \right)^2 = 4\times 10^6 \mathrm{pc}\)走る必要
- \(1000 \mathrm{au}\)以内としても\(40\mathrm{kpc}\)走る必要
(普通の)星同士はまずぶつからない
アンドロメダ銀河との衝突合体
Visualization Credit: NASA, ESA, and F. Summers (STScI)
Simulation Credit: NASA, ESA, G. Besla (Columbia University), and R. van der Marel (STScI)
アンドロメダ銀河との衝突合体
アンドロメダ銀河との衝突合体
おとめ座超銀河団
局部超銀河団
Action Dynamics of the Local Supercluster from Daniel Pomarède on Vimeo.
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/ESA_Gaia_DR2_AllSky_Brightness_Colour_Cartesian_4000x2000.png)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/22-02.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/fg3.h.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/pasj62-1413-g007.gif)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/eso1339e.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/Anatomy_of_the_Milky_Way.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/R0CjB.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/nrao18cb12c.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/xlarge_web.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/nrao18cb12a-2.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/aj268500f15.jpg)
</span>](media/aa25584-14-fig2.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/aa25584-14-fig1.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/Herschel_s_view_of_the_Taurus_molecular_cloud.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/print.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/black-hole-event-horizon-01.adapt.1900.1.jpg)

</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/EHT.jpg)
</span>](http://akari.c.u-tokyo.ac.jp/~doi/Astronomy/media/simulation-1200x600.jpg)
</span>](media/20190410-eht-fig-full.jpg)
</span>](https://www.aanda.org/articles/aa/full_html/2013/09/aa21879-13/aa21879-13-fig2.jpg)
</span>](https://upload.wikimedia.org/wikipedia/commons/7/7a/Tracing_the_origin_of_the_Magellanic_Stream.jpg)
.png)</span>](https://upload.wikimedia.org/wikipedia/commons/5/57/5_Local_Galactic_Group_%28ELitU%29.png)
</span>](http://imgsrc.hubblesite.org/hvi/uploads/image_file/image_attachment/23115/print.jpg)
</span>](http://imgsrc.hubblesite.org/hvi/uploads/image_file/image_attachment/23171/print.jpg)
.png)</span>](https://upload.wikimedia.org/wikipedia/commons/f/fc/6_Virgo_Supercluster_%28ELitU%29.png)